Dimostrazioni

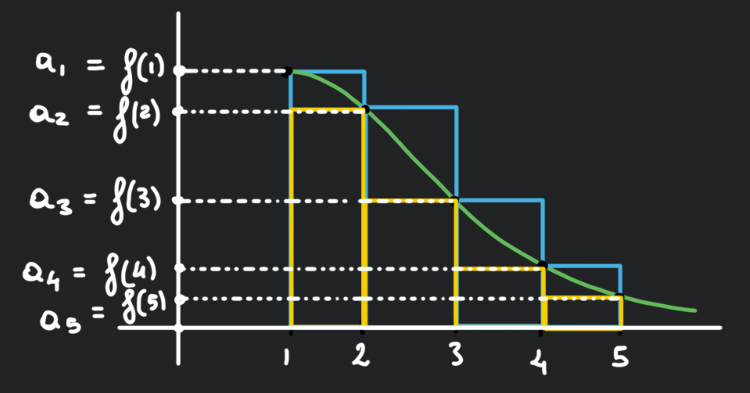
Teorema dell’unicità del limite

Sia $a_n$ una successione , vogliamo dimostrare che ${\lim }_{n\to \infty }{a}_n=l$ dove $l$ è unico :
Supponiamo (per $\text{ASSURDO}$) che

$$\{\begin{array}{l}{\lim }_{n\to \infty }{a}_n=l_1\\ {\lim }_{n\to \infty }{a}_n=l_2\end{array}\text{con}{l}_1\ne l_2$$

passiamo allora alla definizione di limite di successione :

$$\{\begin{array}{llc}\forall ϵ>0& \exists n_1\in \mathbb{N}:|a_n-l_1|<ϵ& \forall n>n_1\\ \forall ϵ>0& \exists n_2\in \mathbb{N}:|a_n-l_2|<ϵ& \forall n>n_2\end{array}$$

adesso prendiamo il massimo tra gli indici di partenza per cui valgono le due disuguaglianze lo stesso , infatti se prendo $n=\max (n_1,n_2)$ , allora valgono sempre lo stesso allo stesso momento siccome vale $\forall n>n_1,n_2$. $⟹$

$$\{\begin{array}{ll}\forall ϵ>0& |a_n-l_1|<ϵ\\ \forall ϵ>0& |a_n-l_2|<ϵ\end{array}$$

ma allora sicuramente abbiamo che :

$$|a_n-l_1|+|a_n-l_2|<ϵ+ϵ=2ϵ$$

adesso utilizziamo la DISUGUAGLIANZA TRIANGOLARE e la proprietà che dice che $|x|=|-x|$ , $⟹$

$$\begin{array}{r}|a_n-l_1|+|l_2-a_n|⟹⟹|a_n-l_1+l_2-a_2|\underset{DT}{\underbrace{\le }}|a_n-l_1|+|a_n-l_2|<2ϵ\\ ⟹|a_n-l_1+l_2-a_n|<2ϵ⟹|l_2-l_1|<2ϵ\end{array}$$

ma scegliendo $ϵ=\frac{|l_2-l_1|}{2}⟹|l_2-l_1|<|l_2-l_1|⟹\text{CONTRADDIZIONE}$

\square$

Teorema del confronto

Vogliamo dimostrare che se $a_n\to l_1$ , $b_n\to l_2$ e

$$\exists n_0\in \mathbb{N}:a_n\le b_n\forall n>n_0$$

( ovvero definitivamente $a_n\le b_n$ ) $⟹l_1\le l_2$ .

Supponiamo per $\text{ASSURDO}$ che $l_1>l_2$ e fissiamo $ϵ=\frac{l_1-l_2}{2}>0$ ( notiamo che è $>0$ siccome abbiamo supposto per assurdo che $l_1>l_2$ ) e applichiamo la definizione per i due limiti :

$$\{\begin{array}{l}\exists n_1\in \mathbb{N}:|a_n-l_1|<ϵ\forall n>n_1\\ \exists n_2\in \mathbb{N}:|b_n-l_2|<ϵ\forall n>n_2\end{array}⟹$$ $$\{\begin{array}{l}\exists n_1\in \mathbb{N}:l_1-ϵ<a_n<l_1+ϵ\forall n>n_1\\ \exists n_2\in \mathbb{N}:l_2-ϵ<b_n<l_2+ϵ\forall n>n_2\end{array}$$

ora prendiamo $n=\max (n_0,n_1,n_2)$ ovvero l’indice di partenza per cui valgono le 3 proprietà ( anche che $a_n\le b_n$ ) e sostituiamo $ϵ=\frac{l_1-l_2}{2}$ otteniamo :

$$l_1-\frac{(l_1-l_2)}{2}=\underbrace{\frac{l_1+l_2}{2}}<a_n<l_1+\frac{(l_1-l_2)}{2}=\frac{3l_1-l_2}{2}$$ $$l_2-\frac{(l_1-l_2)}{2}=\frac{3l_2-l_1}{2}<b_n<l_2+\frac{(l_1-l_2)}{2}=\underbrace{\frac{l_1+l_2}{2}}$$

$⟹$ otteniamo che $b_n<\frac{l_1+l_2}{2}<a_n⟹b_n<a_n\to \text{CONTRADDIZIONE}$
$\square$

Teorema della permanenza del segno

Supponiamo ( caso finito ) che
${\lim }_{n\to \infty }{a}_n=l>0$
Definiamo questo limite attraverso la definizione di limite :

$$\forall ϵ>0\exists n_0\in \mathbb{N}:|a_n-l|<ϵ\forall n>n_0$$

Fissiamo

$$ϵ=\frac{l}{2}>0⟹\exists n_0\in \mathbb{N}:|a_n-l|<\frac{l}{2}\forall n>n_0⟹$$ $$⟹\exists n_0\in \mathbb{N}:l-\frac{l}{2}<a_n<l+\frac{l}{2}\forall n>n_0$$

Poiché $l>0$, anche $\frac{l}{2}>0$, abbiamo che anche

$$a_n>0\forall n>n_0$$

cioè definitivamente ( da un certo $n_0$ in poi ), la successione $a_n$ è positiva.
$\square$

Infinitesima per limitata = 0

Vogliamo dimostrare che se

• $b_n$ è LIMITATA
• ${\lim }_{n\to \infty }{a}_n=0$

$⟹{\lim }_{n\to \infty }{b}_n{a}_n=0$ , che per definizione vuol dire che :

$$\forall ϵ>0\exists n_0\in \mathbb{N}:|b_n{a}_n-0|<ϵ⟹\forall ϵ>0|b_n{a}_n|<ϵ\forall n>n_0$$

---

Iniziamo notando che siccome $b_n$ è LIMITATA allora per definizione $\exists M>0$ tale che :

$$|b_n|\le M⟹-M\le b_n\le M\forall n$$

Inoltre siccome ${\lim }_{n\to \infty }{a}_n=0⟹$

$$\forall \delta >0\exists n_1\in \mathbb{N}:|a_n|<\delta \forall n>n_1$$

utilizziamo ora una prop. dei moduli ( $|ab|=|a||b|$ ) , una catena di disuguaglianze e il fatto che $|b_n|\le M$ :

$$|b_n{a}_n|=|b_n||a_n|\le |a_n|M$$

ora utilizziamo il fatto che $|a_n|<\delta$ e poniamo $\delta =\frac{ϵ}{M}$ , ottenendo :

$$|a_n|M\le \delta M=\frac{ϵ}{\cancel{M}}\cancel{M}$$

quindi otteniamo che

$$|b_n{a}_n|\le |a_n|M\le ϵ$$

$\square$

Convergenza numero di nepero e

Vogliamo dimostrare che la successione $a_n=(1+\frac{1}{n}{)}^n$ è convergente a $e\in (2,3)$ : Dimostriamolo in 2 step :

1. dimostriamo che $a_n=(1+\frac{1}{n}{)}^n$ è STRETTAMENTE CRESCENTE
2. dimostriamo che $a_n=(1+\frac{1}{n}{)}^n$ è SUPERIORMENTE LIMITATA $⟹$ esiste il suo limite e vale $\sup \left\{{\left(1+\frac{1}{n}\right)}^n:n\in {\mathbb{N}}^{+}\right\}\in \mathbb{R}$

Stretta crescenza

Quindi dobbiamo dimostrare che $a_n<a_{n+1}⟹{\left(1+\frac{1}{n}\right)}^n<(1+\frac{1}{n+1}{)}^{n+1}\forall n\ge 1$ esprimiamo $a_n$ con il binomio di Newton ovvero che :

$$(a+b{)}^n=\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})a^{n-k}{b}^k$$

$⟹$

$$a_n={\left(1+\frac{1}{n}\right)}^n=\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)\frac{1}{n^k}=$$ $$=\sum _{k=0}^n\underset{\left(\genfrac{}{}{0ex}{}{n}{k}\right)}{\underbrace{\frac{n(n-1)(n-2)\dots (n-k+1)\cancel{(n-k)!}}{k!\cancel{(n-k)!}}}}\frac{1}{n^k}=$$ $$=\sum _{k=0}^n\frac{1}{k!}\frac{n(n-1)(n-2)\dots (n-k+1)}{n^k}=\sum _{k=0}^n\frac{1}{k!}\left(\underset{=1}{\underbrace{\frac{n}{n}}}\underset{=1-\frac{1}{n}}{\underbrace{\frac{n-1}{n}}}\underset{=1-\frac{2}{n}}{\underbrace{\frac{n-2}{n}}}\dots \underset{=1-\frac{(k-1)}{n}}{\underbrace{\frac{n-k+1}{n}}}\right)$$

quindi otteniamo che :

$$a_n=\sum _{k=0}^n\frac{1}{k!}\left(1\left(1-\frac{1}{n}\right)\dots \left(1-\frac{(k-1)}{n}\right)\right)$$

ora poniamo $n=n+1⟹$ otteniamo :

$$a_{n+1}=\sum _{k=0}^{n+1}\frac{1}{k!}\left(1\left(1-\frac{1}{n+1}\right)\dots \left(1-\frac{(k-1)}{n+1}\right)\right)$$

ora confrontiamo $a_n$ e $a_{n+1}$ , e quindi ci chiediamo le seguenti disuguaglianze :

• $1-\frac{1}{n}\stackrel{?}{\overbrace{<}}1-\frac{1}{n+1}⟹\frac{n-1}{n}<\frac{n}{n+1}⟹\cdots ⟹-\frac{1}{n(n+1)}<0\to \text{SI}$
• $1-\frac{(k-1)}{n}\underset{?}{\underbrace{<}}1-\frac{(k-1)}{n+1}\to \text{SI}$ $⟹a_n<a_{n+1}$

Limitatezza superiore

Lavoriamo sulla sommatoria e otteniamo qualcosa piu grosso :

$$a_n=\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)\frac{1}{n^k}$$

notiamo ( grazie anche allo step precedente ) che :

$$\frac{1}{k!}\underset{\le 1}{\underbrace{1\left(1-\frac{1}{n}\right)\dots \left(1-\frac{(k-1)}{n}\right)}}\le \frac{1}{k!}$$

ma siccome $k!=k(k-1)(k-2)!\ge k(k-1)$ e passando ai reciproci otteniamo che

$$\frac{1}{k!}\le \frac{1}{k(k-1)}=\frac{1}{k-1}-\frac{1}{k}$$

$⟹$

$$a_n=1+1+\sum _{k=2}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)\frac{1}{n^k}\le 2+\sum _{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k}\right)$$

dove l’ultimo termine assomiglia a una serie telescopica , siccome rimane la testa e la coda ( come in un telescopio ) :

$$\sum _{k=2}^n\left(\frac{1}{k-1}-\frac{1}{k}\right)=\left(1-\cancel{\frac{1}{2}}\right)+\left(\cancel{\frac{1}{2}}-\cancel{\frac{1}{3}}\right)+\cdots +\left(\cancel{\frac{1}{n-1}}-\frac{1}{n}\right)=1-\frac{1}{n}$$

quindi possiamo concludere che

$$a_n=2+1-\frac{1}{n}=3-\frac{1}{n}\le 3$$

$⟹$ $a_n$ ha $3$ come maggiorante e dunque è LIMITATA SUPERIORMENTE .

$\square$

Teorema degli zeri

Il teorema dice che sia $f:[a,b]\to \mathbb{R}$ ( definita in un intervallo chiuso e limitato ) e che sia CONTINUA in $[a,b]$ e che $f(a)f(b)<0⟹\exists c\in (a,b):f(c)=0$ . intuitivamente nel grafico abbiamo :

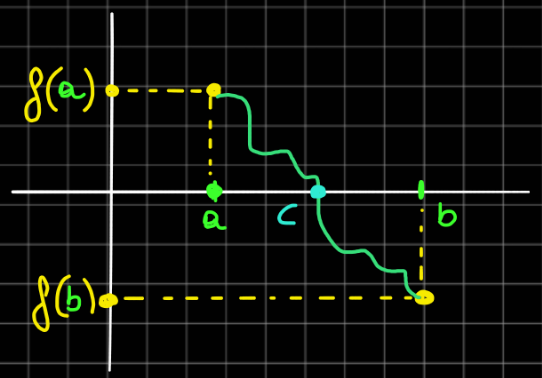
dove se $f(a)>0⟺f(b)<0$ o viceversa , e che siccome la funzione è continua allora sicuramente passerà per un punto $c$ dove assumerà valore $0$.

Costruiamo ricorsivamente due successioni $a_n$ e $b_n$ nel seguente modo ( si pensi come un algoritmo da ripetere ):

$$\{\begin{array}{l}{a}_0=a\\ b_0=b\\ c_1=\frac{a_0+b_0}{2}\end{array}$$

dove $c_1$ è il punto medio del segmento $\overline{ab}$ , quindi ci sono due possibilità :

1. Se $f(c_1)=0⟹c=c_1$ e ho finito
2. Se $f(c_1)\ne 0⟹$ $$\{\begin{array}{l}\text{se}f(a_0)f(c_1)<0⟹a_1=a_0,b_1=c_1(\ast )\\ \text{se}f(b_0)f(c_1)<0⟹a_1=c_1,b_1=b_0(\ast \ast )\end{array}$$ infatti graficamente ( caso $(\ast )$ )

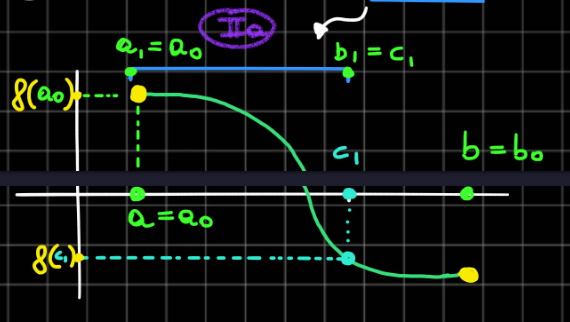
in questo modo considero un intervallo più piccolo $[a,b]=[a_0,c_1]$ di ricerca di questo punto dove la funzione mi farà 0.

Procedendo in questo modo ho definito una successione di intervalli $I_n=[a_n,b_n]$ tale che $I_{n+1}\subseteq I_n$ Inoltre sto garantendo che :

1. $f(a_n)f(b_n)<0\forall n$
2. siccome divido sempre a metà per $n$ volte abbiamo che la lunghezza da i dell’intervallo sarà $b\ast n-a\ast n=\frac{b-a}{2^n}$ Osserviamo inoltre che

• $a_0=a\le a_1\le a_2\le \cdots \le a_n$
• $a_n\le b_n\le \cdots \le b_2\le b_1<b_0=b$ ovvero che $a_n$ va dentro verso destra (quindi cresce) e che $b_n$ va dentro verso sinistra e quindi decresce , quindi ottengo che ho $a_n$ una successione crescente e limitata ( siccome è maggiorata da $b$ e minorata da $a_0$ ) e analogamente $b_n$ è una successione decrescente e limitata. Quindi per il teorema delle successioni monotone, per entrambe le successioni esistono i limiti : $$\{\begin{array}{l}{\lim }_{n\to \infty }{a}_n=c_1\\ {\lim }_{n\to \infty }{b}_n=c_2\end{array}$$ ora devo dimostrare solo che $c_1=c_2$ ( siccome l’intervallo sarà sempre piu piccolo perché $a_n$ entra $\to$ e $b_n$ entra $\leftarrow$)

Quindi siccome devo dimostrare che $c_1=c_2=c$ , allora la differenza dovrebbe fare $0$ , infatti :

$$c_2-c_1=\underset{n\to \infty }{\lim }{b}_n-\underset{n\to \infty }{\lim }{a}_n=\underset{n\to \infty }{\lim }\frac{b-a}{\underset{\to +\infty }{\underbrace{2^n}}}=0$$

Ora dobbiamo dimostrare che $f(c)=0$ e quindi osservo che poiché $f$ è continua in $[a,b]$ allora per definizione di funzione continua in un intervallo :

$$\{\begin{array}{l}f(c)={\lim }_{n\to \infty }f(a_n)\le 0\\ f(c)={\lim }_{n\to \infty }f(b_n)\ge 0\end{array}$$

(oppure viceversa , tanto l’importante è che sappiamo per costruzione che le immagini della funzione in quei punti sono discordi tra loro e quindi il prodotto è negativo) e quindi siccome $f(c)\le 0$ e $f(c)\ge 0$ l’unica possibilità è che $f(c)=0$ . $\square$

Teorema di Weiestrass

Il teorema di Weiestrass ci dice che : sia $f(x):[a,b]\to \mathbb{R}$ :

• Ipotesi :
  • $f$ continua in $[a,b]$
• Tesi :
  • $\exists M=\max f$ e $\exists m=\min f$

Prima di iniziare vero e proprio la dimostrazione , notiamo che $S=\{f(x):\forall x\in [a,b]\}$ siccome è insieme non vuoto, allora sappiamo che

$$\exists s=\sup S$$

ovvero l’estremo superiore dell’insieme $S$. Inoltre sappiamo che esiste una successione $\{y_n{\}}_{n\in \mathbb{N}}$ tale che :

$$\underset{n\to \infty }{\lim }{y}_n=s$$

Infatti nel caso $s\in \mathbb{R}$ , notiamo che $\forall n\in {\mathbb{N}}^{+}\exists y_n\in S$ tale che :

$$s-\frac{1}{n}\le y_n\le s$$

ovvero che comunque prendiamo $n$ troveremo sempre un $y_n$ che sarà più grande di $s-\frac{1}{n}$ ma più piccolo di $s$ , tutto questo per definizione di estremo superiore di un insieme. Però ora siccome $s-\frac{1}{n}\to s$ possiamo applicare il teorema dei carabinieri e concludere che anche $y_n\to s$ .
Nel caso $s=+\infty$ , sappiamo che $\forall n\in \mathbb{N}\exists y_n\in S$ tale che :

$$y_n\ge n$$

anche se $s=+\infty$ cadrebbe la continuità e non il teorema di Weierstrass non vale più.

Iniziamo quindi la dimostrazione costruendo una nuova successione $\{x_n{\}}_{n\in \mathbb{N}}\subseteq [a,b]$ tale che :

$$f(x_n)=y_n\forall n\in \mathbb{N}$$

Ora siccome $x_n$ è una successione limitata allora per il TEOREMA DI BOLZANO-WEIERSTRASS :

$$\exists \{x_n{\}}_k\subseteq \{x_n{\}}_n:\underset{k\to \infty }{\lim }{x}_{n_k}=x_M\in [a,b]$$

ovvero che esiste una sotto-successione $x_{n_k}$ convergente di $x_n$ .

Sappiamo inoltre , grazie alle ipotesi , che $f$ è continua in $[a,b]$ , quindi abbiamo che :

$$\underset{n\to +\infty }{\lim }f(x_n)=f(x_M)\in S$$

Concludiamo che quindi abbiamo :

$$s=\underset{n\to +\infty }{\lim }{y}_n=\underset{n\to +\infty }{\lim }f(x_n)=f(x_M)$$

quindi abbiamo dimostrato che :

$$f(x)\le f(x_M)\in \mathbb{R}\forall x\in [a,b]$$

$\square$

Teorema di Fermat

Il teorema afferma che :

• Ipotesi : sia $f:[a,b]\to \mathbb{R}$
  • $x_0$ sia punto di minimo o massimo relativo
  • $f$ derivabile in $x_0$
• Tesi : $⟹f^{\prime }(x_0)=0$ ossia che $x_0$ è un punto stazionario ( ovvero che la tangente in quel punto è orizzontale )

Dimostriamo nel caso $x_0$ sia un minimo relativo ( similmente per il caso sia massimo relativo )
Iniziamo notiamo che siccome $f$ è derivabile in $x_0$ , allora per definizione di derivabilità in un punto , abbiamo che la derivata destra e sinistra in quel punto devono essere uguali alla derivata in quel punto :

$$f_{+}^{\prime }(x_0)=f_{-}^{\prime }(x_0)=f^{\prime }(x_0)$$

quindi vediamo che segno ha $f_{+}^{\prime }(x_0)$ , infatti notiamo che :

$$f_{+}^{\prime }(x_0)=\underset{h\to 0^{+}}{\lim }=\frac{f(x_0+h)-f(x_0)}{h}$$

quindi vogliamo capire che segno ha $f(x_0+h)-f(x_0)$ . Ora siccome $x_0$ è un minimo relativo , per definizione di minimo relativo :

$$f(x_0)\le f(x)\forall x\in (x-\delta ,x+\delta )$$

quindi sicuramente $f(x_0+h)\ge f(x_0)⟹f(x_0+h)-f(x_0)\ge 0$ , quindi abbiamo che :

$$f_{+}^{\prime }(x_0)=\underset{h\to 0^{+}}{\lim }=\frac{f(x_0+h)-f(x_0)\ge 0}{h\ge 0}⟹f_{+}^{\prime }(x)\ge 0$$

ora similmente per $f_{-}^{\prime }(x_0)$ avremo che :

$$f_{-}^{\prime }(x_0)=\underset{h\to 0^{-}}{\lim }\frac{f(x_0+h)-f(x_0)\ge 0}{h\le 0}⟹f_{-}(x_0)\le 0$$

ma allora abbiamo la seguente situazione di segni :

$$\{\begin{array}{l}{f}^{\prime }(x_0)=f_{+}^{\prime }(x_0)\ge 0\\ f^{\prime }(x_0)=f^{\prime }-(x_0)\le 0\end{array}$$

quindi necessariamente $f^{\prime }(x_0)=0$ .

$\square$

Teorema di Rolle

Il teorema di Rolle afferma che :

• Ipotesi : sia $f(x):[a,b]\to \mathbb{R}$
  • continua in $[a,b]$
  • derivabile in $(a,b)$
  • $f(a)=f(b)$
• Tesi : $⟹\exists c\in (a,b):f^{\prime }(c)=0$ l caso

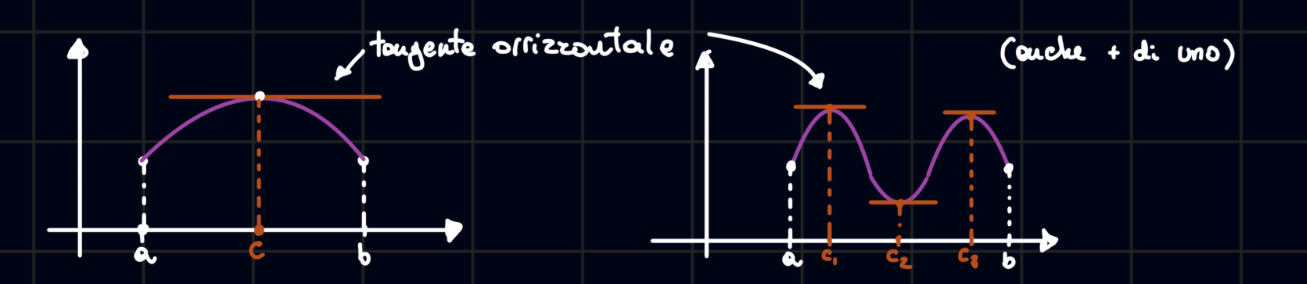
Iniziamo osservando che grazie alle ipotesi possiamo applicare il teorema di Weiestrass infatti abbiamo che :

$$\exists x_m\in [a,b]\exists x_M\in [a,b]:f(x_m)\le f(x)\le f(x_M)\forall x\in [a,b]$$

quindi abbiamo due casi :

1. $x_m$ e $x_M$ sono gli estremi $\{a,b\}⟹f(x_m)=f(x_M)⟹$ otteniamo che $f$ è una funzione costante in $(a,b)$ , ma allora la derivata in ogni punto preso tra $a$ e $b$ , otteniamo che la retta tangente sarà $=0$ infatti avremo che $$f^{\prime }(c)=0\forall x\in (a,b)$$
2. almeno uno dei due di $x_m$ e $x_M$ sono punti interni in $(a,b)$ , ma siccome sono uno un punto di massimo e l’altro un punto di minimo , possiamo applicare il TEOREMA DI FERMAT , infatti avremo che : $$f^{\prime }(x_m)=0\vee f^{\prime }(x_M)=0$$

quindi abbiamo osservato che sia nel caso 1 che nel caso 2 , otteniamo che $\exists c\in (a,b):f^{\prime }(c)=0$

$\square$ .

Teorema di Lagrange o valor medio

Il teorema afferma che :

• Ipotesi : Sia $f:[a,b]\to \mathbb{R}$
  • continua in $[a,b]$
  • derivabile in $(a,b)$
• Tesi : $⟹\exists c\in (a,b):f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}$

dove $\frac{f(b)-f(a)}{b-a}$ sarebbe il coefficiente angolare della retta parallela alla retta tangente nel punto $(c,f(c))$ :

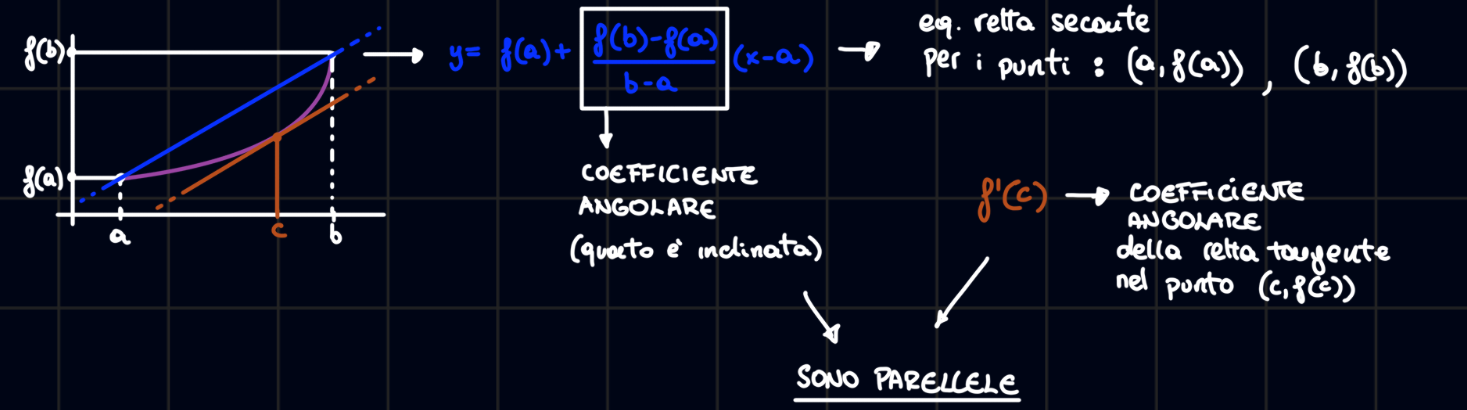
Iniziamo considerando una funzione ausiliaria :

$$h(x)=f(x)-\left(\frac{f(b)-f(a)}{b-a}(x-a)+f(a)\right)$$

calcoliamoci $h(a)$ , $h(b)$ :

$$\{\begin{array}{l}h(a)=f(a)-\frac{f(b)-f(b)}{b-a}(a-a)-f(a)=f(a)-f(a)=0\\ h(b)=f(b)-\frac{f(b)-f(a)}{\cancel{b-a}}\cancel{(b-a)}-f(a)=f(b)-f(b)+f(a)-f(a)=0\end{array}⟹h(a)=h(b)=0$$

Ora siccome abbiamo $h(a)=h(b)$ applichiamo il TEOREMA DI ROLLE , allora abbiamo che :

$$\exists c\in (a,b):h^{\prime }(c)=0$$

( vedi dimostrazione del teorema di Rolle che va usata per dimostrare questo teorema che stiamo dimostrando ).

Ora calcoliamo $h^{\prime }(x)$ ( la derivata ) e poi $h^{\prime }(c)$ , allora abbiamo che :

$$h^{\prime }(x)=f^{\prime }(c)-\left(\frac{f(b)-f(a)}{b-a}\right)⟹h^{\prime }(c)=f^{\prime }(c)-\frac{f(b)-f(a)}{b-a}$$

ma siccome siccome $h^{\prime }(c)=0$ :

$$f^{\prime }(c)-\frac{f(b)-f(a)}{b-a}=0⟹f^{\prime }(c)=\frac{f(b)-f(a)}{b-a}$$

ovvero proprio la nostra tesi .

$\square$ .

Teorema del criterio di monotonia

Il teorema afferma che :

• Ipotesi : sia $f$ derivabile in un intervallo $(a,b)$
• Tesi :
  1. $f$ è CRESCENTE in $(a,b)⟺f^{\prime }(x)\ge 0\forall x\in (a,b)$
  2. $f$ è DECRESCENTE in $(a,b)⟺f^{\prime }(x)\le 0\forall x\in (a,b)$

Dimostriamo 1. ( 2. è simile ) , per dimostrare che vale "$⟺$" dimostriamo prima "$⟹$" e poi "$⟸$" :

"$⟹$"

Quindi per dimostrare che $f^{\prime }(x)\ge 0\forall x\in (a,b)$ dobbiamo capire che segno ha il rapporto incrementale ( che sarebbe per definizione la derivata ) usando l’ipotesi che $f$ è crescente , quindi abbiamo che :

$$f^{\prime }(x)=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}=\{\begin{array}{l}\text{se}h>0⟹f(x+h)\ge f(x)⟹f(x+h)-f(x)\ge 0⟹\left(\frac{+}{+}\right)\ge 0\\ \text{se}h<0⟹f(x+h)\le f(x)⟹f(x+h)-f(x)\le 0⟹\left(\frac{-}{-}\right)\ge 0\end{array}$$

e quindi abbiamo dimostrato che $f^{\prime }(x)$ risulta sempre $\ge 0$ .

"$⟸$"

Ora dobbiamo dimostrare la crescenza di $f$ ovvero che se prendiamo due qualsiasi $x_1,x_2\in (a,b)$ basta che $x_1\le x_2$ , quindi consideriamo questi due punti , e applichiamo il TEOREMA DI LAGRANGE in $[x_1,x_2]\subseteq (a,b)$ , siccome per ipotesi sappiamo che $f$ è derivabile , e quindi questo implica che sia anche continua , in $(a,b)$ e quindi lo è anche $[x_1,x_2]\subseteq (a,b)$ , quindi per il teorema di Lagrange abbiamo che :

$$\exists c\in (x_1,x_2):f^{\prime }(c)=\frac{f(x_2)-f(x_1)}{x_2-x_1}$$

quindi moltiplichiamo a destra e sinistra per per $(x_2-x_1)$ e abbiamo che :

$$f^{\prime }(c)=\frac{f(x_2)-f(x_1)}{x_2-x_1}⟹f^{\prime }(c)(x_2-x_1)=f(x_2)-f(x_1)⟹f(x_2)=f(x_1)+f^{\prime }(c)(x_2-x_1)$$

ma siccome $x_2\ge x_1⟹x_2-x_1\ge 0$ e quindi se aggiungiamo qualcosa di positivo a $f(x_1)$ avremo necessariamente che :

$$f(x_2)\ge f(x_1)$$

che è proprio la crescenza di $f$ .

$\square$ .

Teorema di De l’Hospital

Il teorema di De l’Hospital afferma che :

• Ipotesi : sia $f$ e $g$ funzioni derivabili in $(x_0,x_0+r)r>0$ ( in un intorno destro di $x_0$ ) ($I^{+}(x_0)$)
  • ${\lim }_{x\to x_0^{+}}f(x)={\lim }_{x\to x_0^{+}}g(x)=0$ ( quindi abbiamo una forma $\left[\frac{0}{0}\right]$ )
  • $g^{\prime }(x)\ne 0\forall x\in (x_0,x_0+r)$
  • $\exists {\lim }_{x\to x_0^{+}}\frac{f^{\prime }(x)}{g^{\prime }(x)}=L_1\in \mathbb{R}\cup \{\pm \infty \}$
• Tesi : $⟹{\lim }_{x\to x_0^{+}}\frac{f(x)}{g(x)}=L_1$

Iniziamo la dimostrazione estendendo $f$ e $g$ anche in $x_0$ ponendo $f(x_0)=g(x_0)=0$ in questo modo rendiamo continue $f$ e $g$ anche in $x_0$ . Ora consideriamo una successione $x_n$ in $(x_0,x_0+r)$ tale che $x_n\to x_0^{+}$. Ora notiamo che per $\forall n\in {\mathbb{N}}^{+}$ vale il TEOREMA DI CAUCHY in $[x_0,x_n]$ , che ci dice che siano $f$ e $g$ continue in $[a,b]$ e derivabili in $(a,b)$ e che $g(x)\ne 0\forall x\in (a,b)$ allora sappiamo che :

$$\exists c\in (a,b):\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(c)}{g^{\prime }(c)}$$

.Quindi applicando il teorema di Cauchy in $[x_0,x_n]$ allora abbiamo che :

$$\exists c_n\in (x_0,x_n):\frac{f(x_n)-f(x_0)}{g(x_n)-g(x_0)}=\frac{f^{\prime }(c_n)}{g^{\prime }(c_n)}\forall n\in {\mathbb{N}}^{+}$$

ora notiamo che siccome $f(x_0)=g(x_0)=0$ ( dalle ipotesi ) abbiamo che :

$$\frac{f(x_n)-f(x_0)}{g(x_n)-g(x_0)}=\frac{f(x_n)}{g(x_n)}=\frac{f^{\prime }(c_n)}{g^{\prime }(c_n)}$$

Ora notiamo che siccome $x_0<c_n<x_n$ e $x_n\to x_0^{+}$ , utilizziamo il teorema dei Carabinieri e otteniamo che anche $c_n\to x_0^{+}$.

Infine partiamo dall’ultima ipotesi di esistenza del limite della derivata delle due funzioni :

$$L_1=\underset{x\to x_0^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}$$

e notiamo che possiamo fare un “cambio di variabile” ( o teorema Ponte al contrario ) di $x$ con $c_n$ , siccome tutte e due $\to x_0^{+}$ , quindi abbiamo che :

$$L_1=\underset{x\to x_0^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}=\underset{n\to \infty }{\lim }\frac{f^{\prime }(c_n)}{g^{\prime }(c_n)}$$

ma grazie a Cauchy ( di prima ) abbiamo che :

$$L_1=\underset{x\to x_0^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}=\underset{n\to \infty }{\lim }\frac{f^{\prime }(c_n)}{g^{\prime }(c_n)}\underset{\text{Teo. Cauchy}}{=}\underset{n\to \infty }{\lim }\frac{f(x_n)}{g(x_n)}$$

ora rifacciamo un “cambio di variabile” di $x_n$ con $x$ , siccome anche in questo caso sia una che l’altra $\to x_0^{+}$ , quindi abbiamo che :

$$\underset{n\to \infty }{\lim }\frac{f(x_n)}{g(x_n)}\underset{x_n\to x_0^{+}⟺x\to x_0^{+}}{=}\underset{x\to x_0^{+}}{\lim }\frac{f(x)}{g(x)}$$

quindi abbiamo dimostrato che :

$$L_1=\underset{x\to x_0^{+}}{\lim }\frac{f^{\prime }(x)}{g^{\prime }(x)}=\underset{x\to x_0^{+}}{\lim }\frac{f(x)}{g(x)}$$

$\square$ .

Formula di Taylor con resto di Peano

La formula del polinomio di Taylor con il resto di Peano ci dice che possiamo approssimare una funzione nel seguente modo :

$$f(x)=T_{n,x_0}(x)+R_{n,x_0}(x)$$

ora per capire come dimostrarlo , portiamo $T_{n,x_0}(x)$ a destra e quindi otteniamo :

$$R_{n,x_0}=f(x)-T_{n,x_0}(x)$$

ma siccome il resto di Peano è l’errore commesso dal polinomio di Taylor nell’approssimazione è definito come :

$$R_{n,x_0}(x)=o((x-x_0{)}^n)$$

ovvero proprio quello che vogliamo dimostrare , infatti per definizione di $o$-piccolo :

$$\text{se}{R}_{n,x_0}(x)=o((x-x_0{)}^n)⟹\underset{x\to x_0^{+}}{\lim }\frac{R_{n,x_0}(x)}{(x-x_0{)}^n}=0$$

quindi la dimostrazione consiste nel svolgere un limite e dimostrare che fa $0$. Iniziamo quindi da :

$$\underset{x\to x_0^{+}}{\lim }\frac{R_{n,x_0}(x)}{(x-x_0{)}^n}=\underset{x\to x_0^{+}}{\lim }$$

Criterio della condizione necessaria per la convergenza

Se la serie ${\sum }_{k=0}^{\infty }{a}_k$ è convergente $⟹{\lim }_{n\to \infty }{a}_n=0$ ( quindi si fa il test del limite , se $\ne 0$ allora possiamo dire che non converge )

Per ipotesi sappiamo che la serie converge $⟹$ ${\lim }_{n\to \infty }{S}_n=S\in \mathbb{R}$

se facciamo un passo indietro e quindi per $S_{n-1}$ $⟹{\lim }_{n\to \infty }{S}_{n-1}=S\in \mathbb{R}$ (converge lo stesso non frega niente se faccio un passo in indietro tanto $n\to \infty$ ) quindi abbiamo :

$$\underset{n\to \infty }{\lim }{S}_n-S_{n-1}=S-S=0$$

inoltre notiamo che :

$$\begin{array}{r}{S}_n-S_{n-1}=\\ =(\cancel{a_0+a_1}+\cdots +\cancel{an-1}+a_n)-(\cancel{a_0+a_1}+\cdots +\cancel{a_{n-1}})\\ =a_n⟹\underset{n\to \infty }{\lim }{S}_n-S_{n-1}=\underset{n\to \infty }{\lim }{a}_n=0\end{array}$$

Criterio di Leibniz

Il Criterio di Leibniz dice :

• IPOTESI : Sia $a_n$ una successione in $\mathbb{R}$ e
  • $a_n\ge a_{n+1}$ ( decrescente , anche definitivamente )
  • ${\lim }_{n\to \infty }{a}_n=0$
  • $a_n\ge 0\forall n\in \mathbb{N}$
• TESI : La serie ${\sum }_{n=0}^{\infty }(-1{)}^n{a}_n<\infty$ ( converge )

Dimostriamo quindi che la serie converge considerando la somma parziale $S_n={\sum }_{k=0}^n(-1{)}^k{a}_k$ e quindi che il ${\lim }_{n\to \infty }{S}_n<\infty$ , facciamo tutto in step :

• decrescenza di $S_{2n}$ ( somma parziale dei termini pari ) : $S_{2n+2}\le S_{2n}$ ( il successivo è piu piccolo del precedente )
• crescenza di $S_{2n-1}$ ( somma parziale dei termini dispari ) : $S_{2n+1}\ge S_{2n-1}$ ( il successivo è piu grande del precedente )
• $S_{2n}$ è limitata inferiormente
• $S_{2n-1}$ è limitata superiormente
• limiti di $S_{2n}$ e $S_{2n-1}$ sono uguali

Osserviamo prima che “andamento” ha la somma parziale e infatti notiamo che :

$$\begin{array}{r}{S}_n=\sum _{k=0}^n(-1{)}^k{a}_k=a_0-a_1+a_2-a_3+a_4-a_5+\dots \end{array}$$ $$\{\begin{array}{l}{S}_0=a_0\\ S_1=S_0-a_1\\ S_2=S_1+a_2\\ S_3=S_2-a_3\\ S_4=S_3+a_4\\ \dots \end{array}$$

quindi notiamo che

$$\{\begin{array}{l}{S}_{2n+2}=S_{2n+1}+a_{2n+2}\\ S_{2n+1}=S_{2n}-a_{2n+1}\end{array}$$

Decrescenza di $S_{2n}$

Notiamo che per la somma parziale pari ( $2n+2$ )

$$S_{2n+2}=\underbrace{S_{2n+1}}+a_{2n+2}=\underbrace{S_{2n}-a_{2n+1}}+a_{2n+2}$$

ma siccome per l’ipotesi che la successione è decrescente ( il successivo è piu piccolo del precedente ) :

$$a_{2n+2}\le a_{2n+1}⟹-a_{2n+1}+a_{2n+2}\le 0$$

quindi se sommo a $S_{2n}$ qualcosa di negativo allora il risultato sarà $\le S_{2n}$ , quindi abbiamo che :

$$S_{2n+2}=S_{2n}-a_{2n+1}+a_{2n+2}\le S_{2n}⟹S_{2n+2}\le S_{2n}$$

Crescenza di $S_{2n-1}$

Quindi analogamente notiamo che :

$$S_{2n+1}=\underbrace{S_{2n}}-a_{2n+1}=\underbrace{S_{2n-1}+a_{2n}}-a_{2n+1}\ge S_{2n-1}⟹S_{2n+1}\ge S_{2n-1}$$

Limitatezza superiore e inferiore

Quindi ora notiamo che :

$$S_{2n}=S_{2n-1}+a_{2n}\ge S_{2n-1}⟹S_{2n}\ge S_{2n-1}$$

quindi grazie alla decrescenza di $S_{2n}$ ( pari ) e crescenza di $S_{2n-1}$ ( dispari ) , e notiamo che :

$$\underset{S_{2n+1}\le S_{2n-1}}{\underbrace{S_1\le S_{2n-1}}}\le \underset{S_{2n}\le S_{2n+2}}{\underbrace{S_{2n}\le S_0}}$$

( questa situazione è la stessa nel disegno ) Quindi siccome $S_{2n}$ è limitata superiormente e monotona crescente , per il teorema della successione monotona limitata inferiormente esiste il limite finito ( converge ) , analogamente per $S_{2n-1}$ ( ma per teorema inverso ) :

$$\exists \underset{n\to \infty }{\lim }{S}_{2n}=L_0\wedge \exists \underset{n\to \infty }{\lim }{S}_{2n-1}=L_1$$

$L_0=L_1$

Per dimostrare che $L_0=L_1$ , portiamo di la :

$$L_0-L_1=\underset{n\to \infty }{\lim }(S_{2n}-S_{2n-1})$$

ma siccome :

$$S_{2n}=S_{2n-1}+a_{2n}⟹S_{2n}-S_{2n-1}=a_{2n}$$

quindi abbiamo che

$$L_0-L_1=\underset{n\to \infty }{\lim }{a}_{2n}=0$$

dove nell’ultimo passaggio abbiamo usato l’ipotesi del criterio che $a_n\to 0$ .

Quindi abbiamo dimostrato che i due limiti sono uguali , e che quindi siccome le due somme parziali unendole otteniamo $S_n$ ( $\{S_{2n}\}\cup \{S_{2n-1}\}=S_n$ ) , abbiamo dimostrato che $S_n\to L\in \mathbb{R}$ converge.

$\square$

Limite notevole $\frac{\sin (x)}{x}$

Vogliamo dimostrare che ${\lim }_{x\to 0}\frac{\sin (x)}{x}=1$ : quindi siccome la funzione $\frac{\sin (x)}{x}$ risulta pari basta anche fare per $x\to 0^{+}$ e notiamo che per $x>0$ ( basta di poco infatti ) , $\sin (x)\ge 0$ e quindi notiamo che

$$\begin{array}{r}0\le \sin (x)\le x\le \tan (x)=\frac{\sin (x)}{\cos (x)}⟹\text{divido tutto per}\sin (x)⟹0\le 1\le \frac{x}{\sin (x)}\le \frac{1}{\cos (x)}\\ ⟹1\le \frac{x}{\sin (x)}\le \frac{1}{\cos (x)}⟹\text{passo per i reciproci}⟹\cos (x)\le \frac{\sin (x)}{x}\le 1⟹\end{array}$$

siccome

$$\underset{\to 1\text{per}x\to 0^{+}}{\underbrace{\cos (x)}}\le \frac{\sin (x)}{x}\le \underset{\to 1}{\underbrace{1}}$$

allora per il teorema dei Carabinieri anche $\frac{\sin (x)}{x}\to 1$ per $x\to 0^{+}$. $\square$

Disuguaglianza di Bernoulli

Vogliamo dimostrare che

$$\forall n\ge 1(\in {\mathbb{N}}^{+})\forall x\ge -1(1+x{)}^n\ge 1+nx$$

Dimostrazione per $\text{INDUZIONE}$ su $n$ : PB : $P(1)⟹(1+x{)}^1\ge 1+x⟹\text{VERO}$ PI : Sappiamo quindi da PB che $P(n):(1+x{)}^n\ge 1+nx$ è VERA allora dimostriamo che è VERA anche

$$P(n+1):(1+x{)}^{n+1}\ge 1+(n+1)x\text{per}n\ge 1$$

Iniziamo e notiamo che

$$(1+x{)}^{n+1}=(1+x)(1+x{)}^n\underset{P(n)}{\underbrace{\ge }}(1+x)(1+nx)=1+nx+x+n{x}^2=1+(1+n)x+n{x}^2$$

quindi ora ci chiediamo se

$$1+(n+1)x+n{x}^2\underset{?}{\underbrace{\ge }}1+(n+1)x⟹?=\text{si ovvio}$$

$\square$ .

Potenza di un binomio

Vogliamo dimostrare per $\text{INDUZIONE}$ che

$$\forall a,b\in \mathbb{R}\forall n\in {\mathbb{N}}^{+}(a+b{)}^n=\sum _{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})a^{n-k}{b}^k$$

Partiamo con il passo base :

$$\begin{array}{r}P(1):(a+b{)}^1=\sum _{k=0}^1(\genfrac{}{}{0ex}{}{1}{k})a^{n-k}+b^k=\\ =\left(\genfrac{}{}{0ex}{}{1}{0}\right)a^{1-0}{b}^0+\left(\genfrac{}{}{0ex}{}{1}{1}\right)a^{1-1}{b}^1=\\ =a+b⟹P(n)\text{eˋ VERA}\end{array}$$

Ora passiamo al passo induttivo :

• Ipotesi induttiva $\to P(n):(a+b{)}^n={\sum }_{k=0}^n(\genfrac{}{}{0ex}{}{n}{k})a^{n-k}{b}^k$
• Tesi induttiva $\downarrow$ $$P(n+1):\underset{LHS}{\underbrace{(a+b{)}^{n+1}}}=\underset{RHS}{\underbrace{\sum _{k=0}^{n+1}\left(\genfrac{}{}{0ex}{}{n+1}{k}\right)a^{n+1-k}{b}^k}}$$

Quindi iniziamo da $LHS$ per arrivare a $RHS$ e notiamo - utilizzando $P(n)$ - che :

$$(a+b{)}^{n+1}=(a+b)(a+b{)}^n=(a+b)\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{n-k}{b}^k$$

ora distribuiamo $a$ e $b$ con la sommatoria e abbiamo che :

$$(a+b)\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{n-k}{b}^k=\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{(n+1)-k}{b}^k+\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{n-k}{b}^{k+1}$$

ora lasciamo la prima sommatoria uguale e facciamo uno “shift” di indice per la seconda sommatoria , quindi passiamo da $k=0\to k=1$ e quindi anche $n\to n+1$ , ricordiamo però che ora nella seconda sommatoria ogni $k$ diventa $k-1$ :

$$\begin{array}{r}\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{(n+1)-k}{b}^k+\sum _{k=1}^{n+1}\left(\genfrac{}{}{0ex}{}{n}{k-1}\right)a^{n-(k-1)}{b}^{(k-1)+1}=\\ =\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{(n+1)-k}{b}^k+\sum _{k=1}^{n+1}\left(\genfrac{}{}{0ex}{}{n}{k-1}\right)a^{(n+1)-k}{b}^k\end{array}$$

ora “tiriamo fuori” dalla prima sommatoria il primo termine ( $k=0$ ) e dalla seconda sommatoria l’ultimo termine ( $k=n+1$ ) ( per poter “allineare” le due sommatorie e poi riunirle in una sola ) :

$$\begin{array}{r}\left(\genfrac{}{}{0ex}{}{n}{0}\right)a^{n+1}{b}^0+\sum _{k=1}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{(n+1)-k}{b}^k+\sum _{k=1}^n\left(\genfrac{}{}{0ex}{}{n}{k-1}\right)a^{(n+1)-k}{b}^k+\left(\genfrac{}{}{0ex}{}{n+1}{n+1}\right)a^{n-(n+1-1)}{b}^{n+1}=\\ a^{n+1}+\sum _{k=1}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)a^{(n+1)-k}{b}^k+\sum _{k=1}^n\left(\genfrac{}{}{0ex}{}{n}{k-1}\right)a^{(n+1)-k}{b}^k+b^{n+1}\end{array}$$

dove nell’ultimo passaggio abbiamo utilizzato che $\left(\genfrac{}{}{0ex}{}{n}{0}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{n+1}\right)=1$ . Ora siccome le due sommatorie partono e finiscono dagli stessi numeri ( sono “allineate” ) , possiamo unirle in una sola :

$$a^{n+1}+b^{n+1}+\sum _{k=1}^n\left(\left(\genfrac{}{}{0ex}{}{n}{k}\right)+\left(\genfrac{}{}{0ex}{}{n}{k-1}\right)\right)a^{n+1-k}{b}^k$$

Ora utilizziamo la REGOLA DI PASCAL che dice che :

$$\left(\genfrac{}{}{0ex}{}{n}{k}\right)+\left(\genfrac{}{}{0ex}{}{n}{k-1}\right)=\left(\genfrac{}{}{0ex}{}{n+1}{k}\right)$$

quindi abbiamo che :

$$a^{n+1}+b^{n+1}+\sum _{k=1}^n\left(\genfrac{}{}{0ex}{}{n+1}{k}\right)a^{n+1-k}{b}^k$$

ora l’ultimo passo è “rimettere dentro” i due termini esterni tirati fuori prima , quindi dobbiamo ripartire con $k=0$ e finire fino a $n+1$ e quindi otteniamo proprio $RHS$ :

$$\sum _{k=0}^{n+1}\left(\genfrac{}{}{0ex}{}{n+1}{k}\right)a^{n+1-k}{b}^k$$

$\square$ .

$\sqrt{2}\notin \mathbb{Q}$

Vogliamo dimostrare che $\sqrt{2}\notin \mathbb{Q}$ e che quindi siano $a,b$ irriducibili , $\sqrt{2}$ non può essere scritto come $\frac{a}{b}$ , ma allora per dimostrare che $\sqrt{2}\notin \mathbb{Q}$ , supponiamo per $\text{ASSURDO}$ che $\sqrt{2}\in \mathbb{Q}⟹$ $\sqrt{2}$ può essere scritto come $\frac{a}{b}$ $⟹$ $\sqrt{2}=\frac{a}{b}$ , ora eleviamo tutto al quadrato e quindi $2=\frac{a^2}{b^2}⟹a^2=2b^2⟹\underset{\text{pari}}{\underbrace{a^2}}=\underset{\text{pari}}{\underbrace{2b^2}}$ , ma se $a^2$ è pari allora anche $a$ è pari , quindi possiamo chiamare $a=2c$ $⟹(2c{)}^2=2b^2⟹4c^2=2b^2⟹2c^2=b^2⟹\underset{\text{pari}}{\underbrace{2c^2}}=\underset{\text{pari}}{\underbrace{b^2}}$ ma se $b^2$ è pari allora anche $b$ è pari. Quindi abbiamo ottenuto che sia $a$ e $b$ sono pari , da questo otteniamo una $\text{CONTRADDIZIONE}$ , siccome le nostre ipotesi erano che $a$ e $b$ erano “irriducibili” fra di loro , ovvero che erano coprimi, ovvero che non hanno nessun divisore in comune. coprimi

Teorema della media Integrale

Il teorema della media integrale afferma che :

• Ipotesi : Sia $f:[a,b]\to \mathbb{R}$
  • continua in $[a,b]$ e quindi integrabile in $[a,b]$
• Tesi : $⟹\exists c\in [a,b]:$ $$\frac{1}{b-a}{\int }_a^{b}f(x)dx=f(c)⟹f(c)(b-a)={\int }_a^{b}f(x)dx$$

Iniziamo , osservando che siccome $f$ è continua in $[a,b]$ allora per il TEOREMA DI WEIERSTRASS , sappiamo che esistono il massimo e il minimo :

$$\exists m,M\in \mathbb{R}:m\le f(x)\le M\forall x\in [a,b]$$

Ora possiamo osservare che se consideriamo una partizione dei soli punti $x_0=a<b=x_1$ , che chiamiamo $\sigma$ , possiamo dire che allora che :

$$s(f,\sigma )=m(b-a)\le {\int }_a^{b}f(x)dx\le M(b-a)=S(f,\sigma )$$

ma allora dividendo tutto per $(b-a)$ otteniamo che :

$$m\le \frac{1}{b-a}{\int }_a^{b}f(x)dx\le M$$

ora siccome $\frac{1}{b-a}{\int }_a^{b}f(x)dx$ si trova tra $m$ e $M$ , per il TEOREMA DEI VALORI INTERMEDI abbiamo che :

$$\exists c\in [a,b]:f(c)=\frac{1}{b-a}{\int }_a^{b}f(x)dx$$

$\square$ .

Teorema del calcolo Integrale

Il teorema del calcolo integrale afferma che :

• Ipotesi : sia $f$ continua in $[a,b]$ e definita la funzione $I(x):[a,b]\to \mathbb{R}$ , dove : $$I(x):{\int }_a^{x}f(t)dt$$
• Tesi : 1. $I$ è derivabile in $[a,b]$ e $I^{\prime }(x)=f(x)$ ( ovvero che $I$ è una primitiva di $f$ ) 2. sia $F$ una qualsiasi primitiva di $f$ ovvero che $F^{\prime }(x)=f(x)$ allora abbiamo che : $${\int }_a^{b}f(x)dx={\left[F(x)\right]}_a^b=F(b)-F(a)$$

Tesi 1

Vogliamo dimostrare che data la funzione $I(x)$ definita come nelle ipotesi , allora $I$ è derivabile in $[a,b]$ ed è una primitiva di $f$ , quindi dobbiamo “lavorare” con il rapporto incrementale di $I(x)$ , quindi consideriamo $x,x+h\in [a,b]$ con $h\ne 0$ , quindi abbiamo che

$$\begin{array}{r}{I}^{\prime }(x)=\underset{h\to 0}{\lim }\frac{I(x+h)-I(x)}{h}=\\ =\frac{1}{h}\left[{\int }_a^{x+h}f(t)dt-{\int }_a^{x}f(t)dt\right]\underset{\text{linearitaˋ}}{=}\\ =\frac{1}{h}\left[\cancel{{\int }_a^{x}f(t)dt}+{\int }_x^{x+h}f(t)dt-\cancel{{\int }_a^{x}f(t)dt}\right]\end{array}$$

quindi otteniamo che :

$$\underset{h\to 0}{\lim }\frac{1}{h}{\int }_x^{x+h}f(t)dt$$

ora osserviamo che possiamo applicare il TEOREMA DELLA MEDIA INTEGRALE in $[x,x+h]$ , quindi otteniamo che :

$$\exists c(h)\in [x,x+h]:f(c(h))=\frac{1}{\cancel{x}+h-\cancel{x}}{\int }_x^{x+h}f(t)dt$$

ma siccome $x\le c(h)\le x+h$ allora per confronto anche $c(h)\to x$ per $h\to 0$ , quindi otteniamo che :

$$I^{\prime }(x)=\underset{h\to 0}{\lim }\frac{1}{h}{\int }_x^{x+h}f(t)dt=\underset{h\to 0}{\lim }f(c(h))=f(x)$$

ovvero proprio la nostra tesi 1. .

Tesi 2

Vogliamo dimostrare che se prendiamo una qualsiasi primitiva di $f$ ovvero $F$ allora possiamo usare la formula ( mostrata nella tesi 2. ) per calcolare l’integrale. Quindi per dimostrare la tesi 2 , possiamo partire dal fatto che $F$ è una primitiva , quindi vuol dire che $F(x)=I(x)+c$ , siccome anche $I(x)$ per 1. è una primitiva di $f$ . Quindi possiamo osservare che :

$$\begin{array}{r}F(b)-F(a)=I(b)+\cancel{c}-I(a)-\cancel{c}\underset{\text{def di I(x)}}{=}\\ ={\int }_a^{b}f(x)dt-\underset{=0}{\underbrace{{\int }_a^{a}f(x)dx}}={\int }_a^{b}f(x)dx\end{array}$$

ovvero la nostra tesi 2 . $\square$ .

Teorema del confronto integrale

Il teorema afferma che:

• Ipotesi : siano $f$ e $g$ funzioni
  • continue in $[a,b)$ con $b\in \mathbb{R}\cup \{\pm \infty \}$
  • integrabili in $[a,t]\forall t\in (a,b)$
  • $0\le f(x)\le g(x)\forall x\in [a,b)$
• Tesi :
  • se ${\int }_a^{b}g(x)dx$ converge $⟹{\int }_a^{b}f(x)dx$ converge
  • se ${\int }_a^{b}f(x)dx$ diverge $⟹{\int }_a^{b}g(x)dx$ diverge

Osservazione preliminare

Prima di dimostrare il teorema abbiamo bisogno di una osservazione fondamentale , ovvero che : sia $f:[a,b)\to \mathbb{R}$ con $b\in \mathbb{R}\cup \{\pm \infty \}$ , e tale che $f$ sia integrabile in qualsiasi punto $c\in [a,b)$ ( ovvero che comunque prendo un punto $c\in [a,b)$ posso fare l’integrale della funzione ) e $f(x)\ge 0\forall x\in [a,b)$ , sappiamo che anche la funzione integrale $F(t)$ , definita come :

$$F(t)={\int }_a^{t}f(x)dx$$

sarà crescente in $[a,b)$. Infatti se considero due punti $t_1,t_2$ tale che $a\le t_1<t_2<b$ allora ottengo che :

$$F(t_2)-F(t_1)={\int }_{t_1}^{t_2}f(x)dx\ge 0⟹F(t_2)\ge F(t_1)$$

dove nell’ultimo passaggio deduciamo che anche ${\int }_{t_1}^{t_2}f(x)dx\ge 0$ siccome anche la funzione $f(x)\ge 0$ in $[a,b)$.

( inoltre notiamo che partiamo da $F(t_2)-F(t_1)$ per capire che segno ha in modo da dedurre che è crescente , ovvero che comunque prendo due punti $t_1<t_2$ devo ottenere che $F(t_2)\ge F(t_1)$ )

Quindi se ho una funzione $F(t)$ crescente in $[a,b]$ , allora ammette limite :

$$\underset{t\to b^{-}}{\lim }F(t)=\underset{t\to b^{-}}{\lim }{\int }_a^{t}f(x)dx\underset{\text{def di integrale improprio}}{=}{\int }_a^{b}f(x)dx$$

Dimostrazione

Ora dimostriamo il teorema considerando due funzioni $F(t)$ e $G(t)$ nel seguente modo :

$$F(t)={\int }_a^{t}f(x)dx\wedge G(t)={\int }_a^{t}g(x)dx$$

ora siccome abbiamo la relazione ( ipotesi ) che $0\le f(x)\le g(x)\forall x\in [a,b)$ , allora necessariamente con $a\le t<b$ abbiamo che anche le due funzioni definite seguono la stessa “relazione” :

$$0\le F(t)\le G(t)⟹0\le {\int }_a^{t}f(x)dx\le {\int }_a^{t}g(x)dx$$

ma siccome grazie all’osservazione preliminare e alla permanenza del segno dei limiti , sappiamo che : $F(t),G(t)$ sono funzioni crescenti allora ammettono limiti , quindi avremo che :

$$0\le \underset{t\to b^{-}}{\lim }{\int }_a^{t}f(x)dx\le \underset{t\to b^{-}}{\lim }{\int }_a^{t}g(x)dx$$

ma per definizione di integrale improprio otteniamo che :

$$0\le {\int }_a^{b}f(x)dx\le {\int }_a^{b}g(x)dx$$

e da questo otteniamo la tesi. $\square$

Teorema del confronto integrali - serie