NS Diagrams

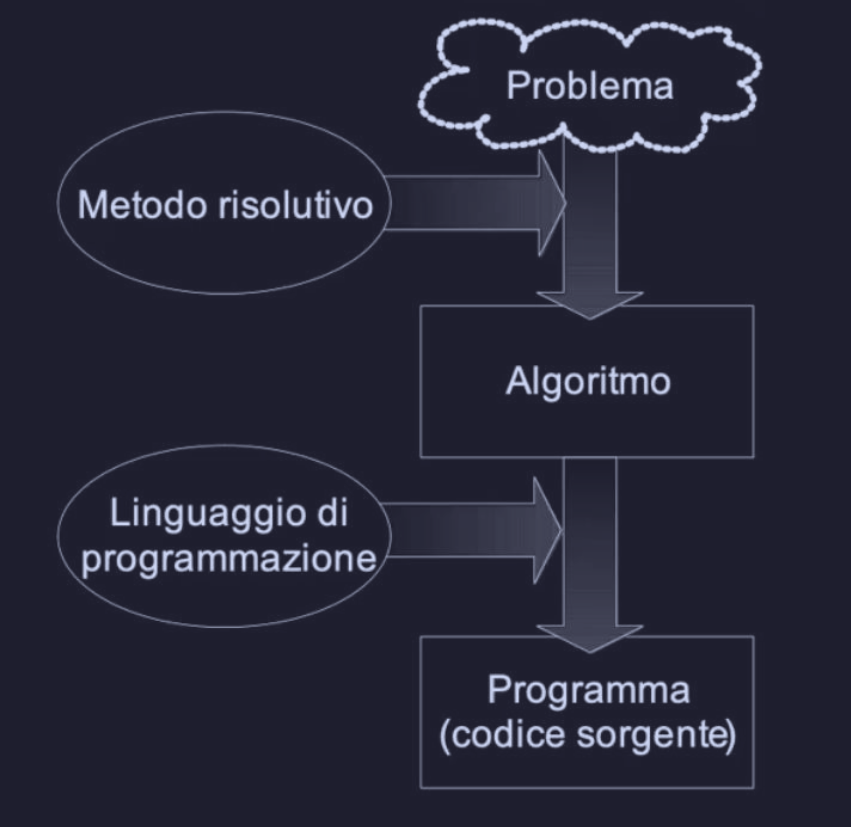
Inizialmente è difficile scrivere immediatamente un algoritmo perfettamente funzionante, e quindi prima di raggiungere il funzionamento atteso di un algoritmo, bisogna procedere per tentativi.

Una volta definito il compito dell’algoritmo bisogna, circoscrivere l’ambiente in cui esso opera. Quindi bisogna specificare i parametri in ingresso e i parametri in uscita. Questa fase di definizione dei requisiti serve a definire il contratto tra il metodo (funzione) che risolve il problema attraverso un algoritmo e il mondo esterno.

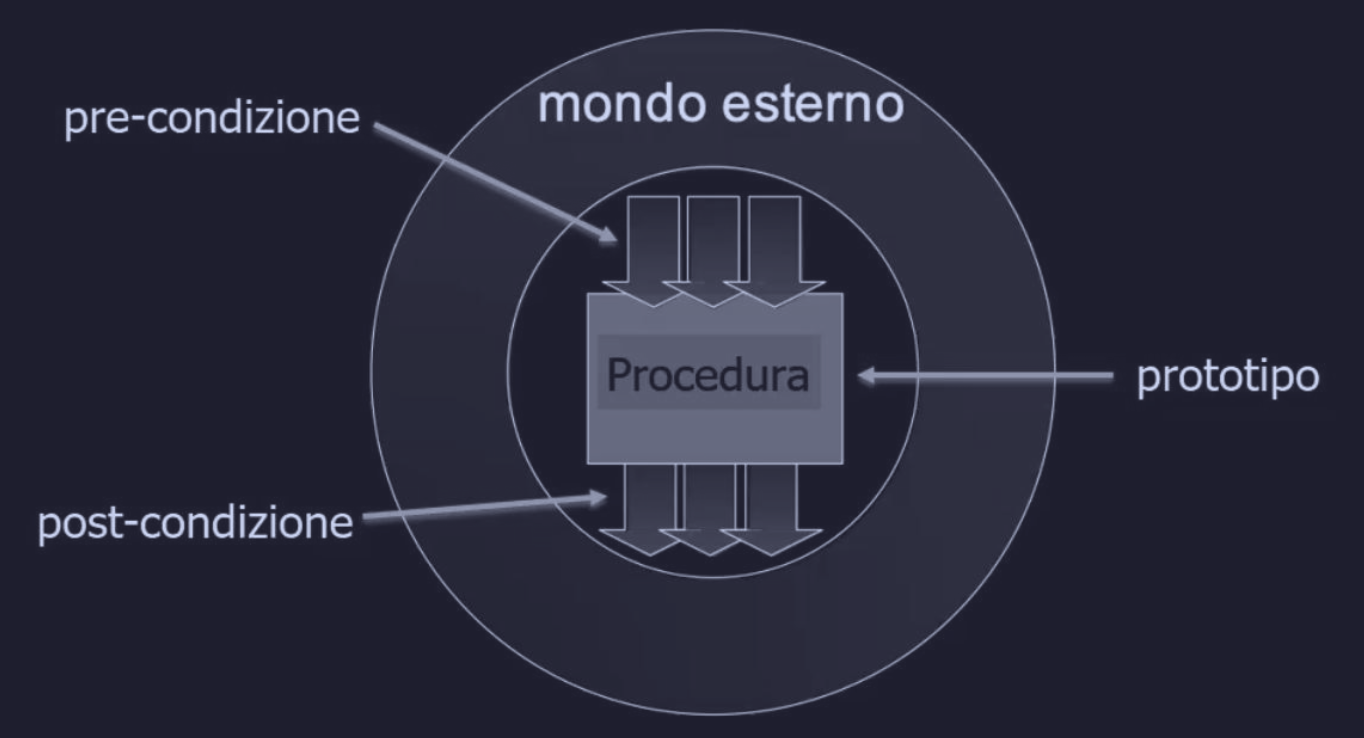
In generale gli algoritmi possono essere descritti con dei diagrammi, come i flow chart.

Vediamo ora un esempio di algoritmo :

Descrivere requisiti (obiettivi e contratto) e metodo dell'algoritmo che riceve in ingresso due array ordinati in modo crescente ( v e w) e restituisce in uscita un nuovo array con all'interno l'insieme ordinato degli elementi dei due array originari.

L’obiettivo quindi è il seguente (esempio) :

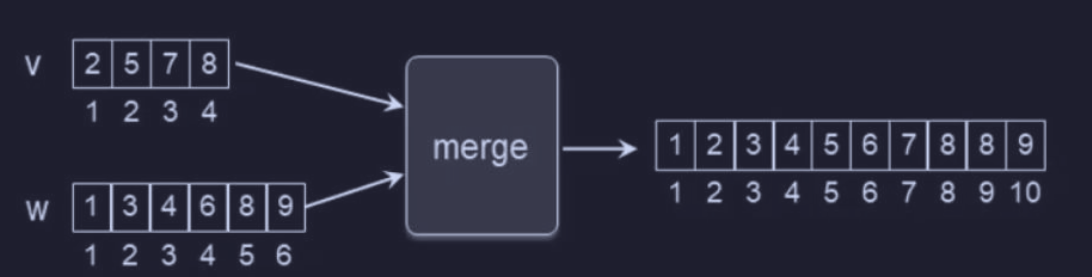
quindi possiamo dire che :

• contratto :

int[] merge(int[] v, int[] w) 

• pre-condizione : v e w sono ordinati in modo crescente
• post-condizione : restituire un nuovo array ordinato in modo crescente con gli elementi di v e w

Possiamo risolvere il problema in questo modo :

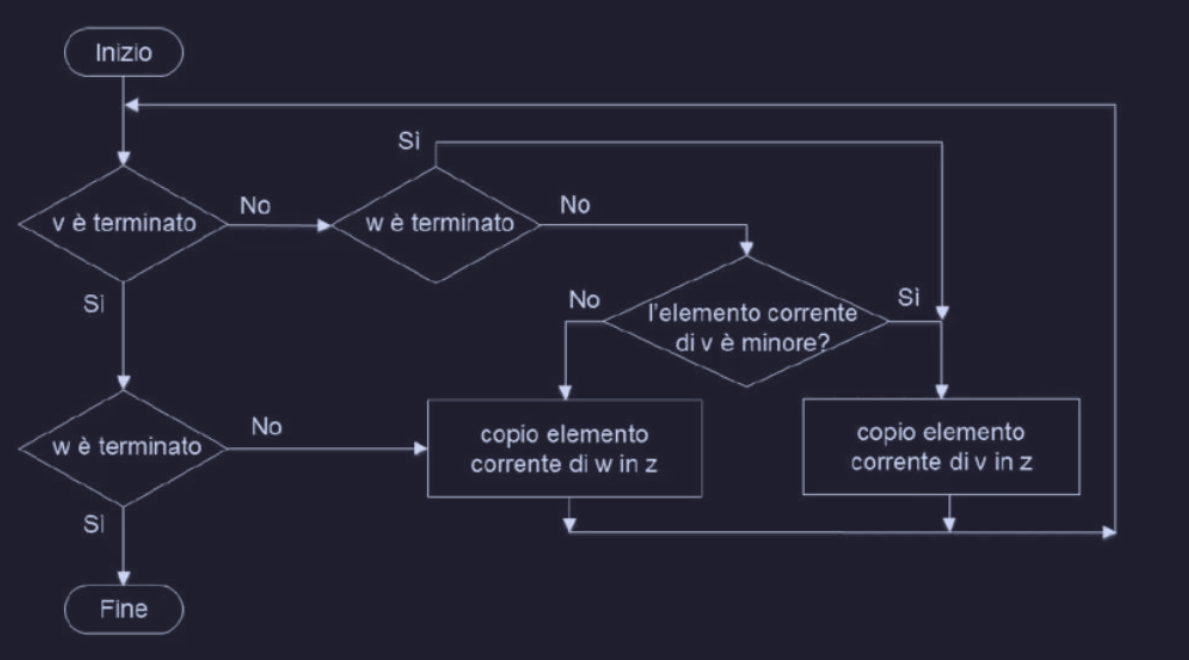
oppure se assumiamo che le lunghezze di v e w siano n e m (rispettivamente) :

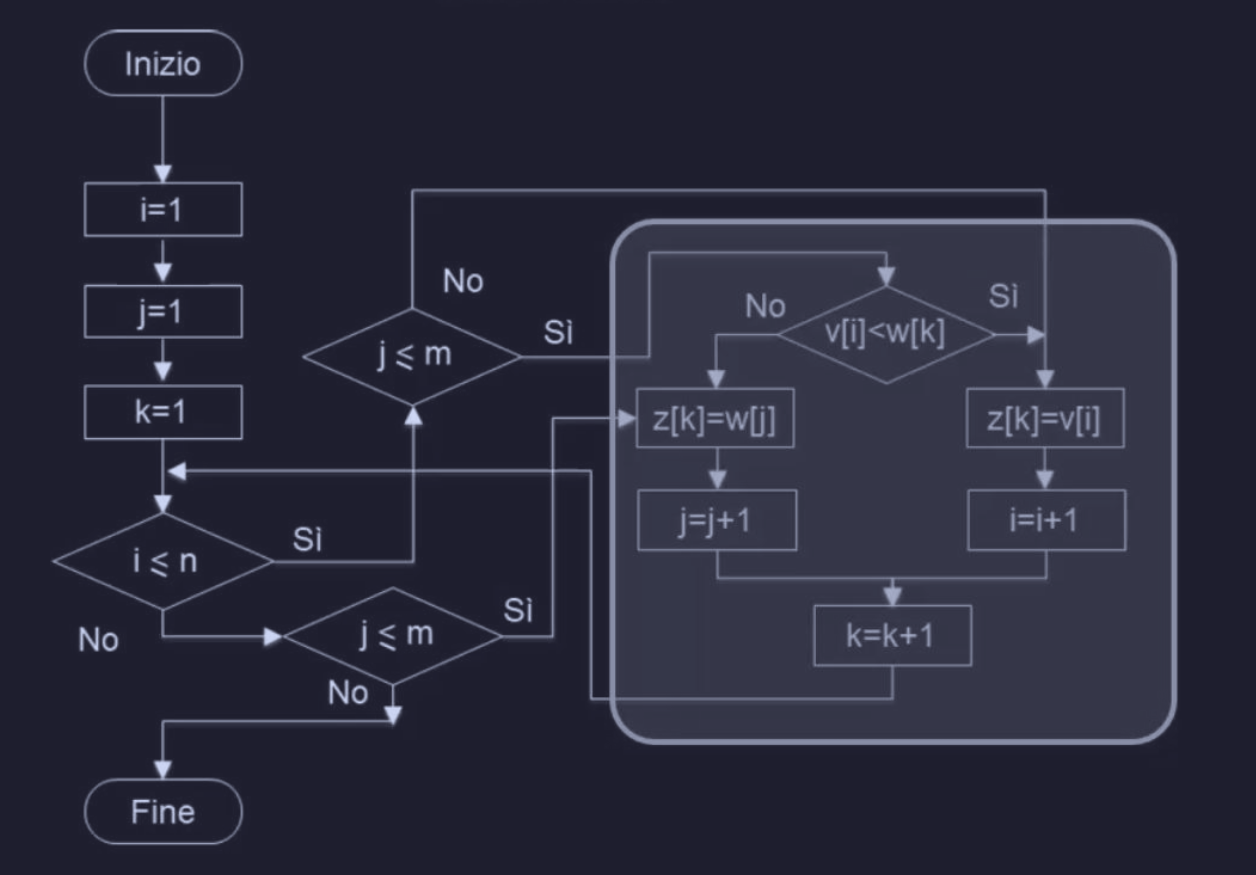
Diagrammi Nassi-Shneiderman - NS

Grazie al formalismo ideato da Isaac Nassi e Ben Shneiderman, abbiamo uno strumento semplice per scrivere algoritmi ben strutturati e ben formati dal punto di vista dell’indentazione del codice. Questo formalismo è rappresentato da dei diagrammi chiamati NS Diagrams (Nassi-Shneiderman Diagrams).

Quindi qualsiasi metodo risolutivo può essere realizzato in una forma strutturata utilizzando :

• la sequenza
• la selezione
• l’iterazione

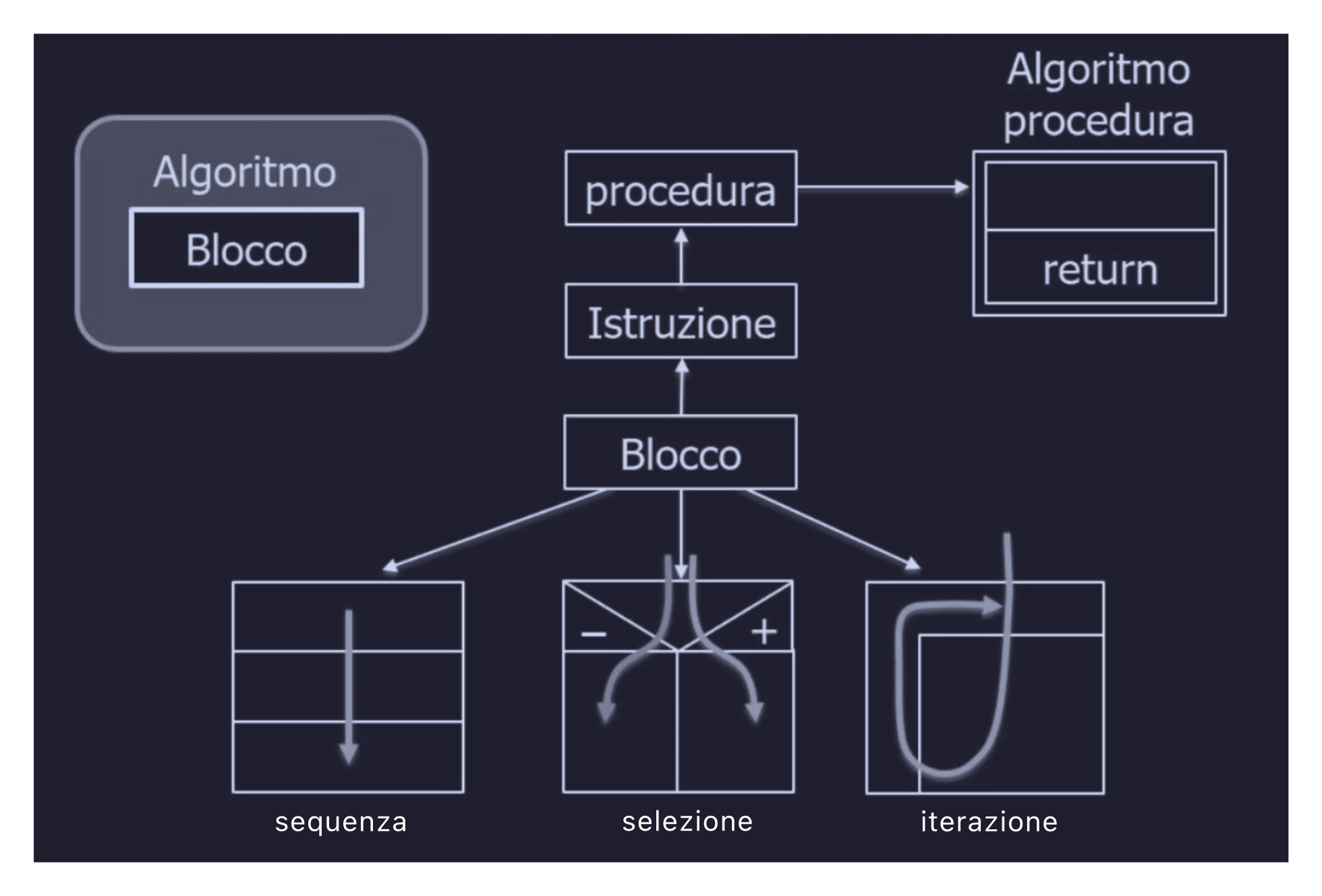
Sequenza

Rappresenta una singola istruzione, o un gruppo di operazioni che vengono eseguite in modo sequenziale.

Selezione

La selezione è un blocco attraverso il quale il flusso di esecuzione può prende percorsi diversi a seconda di una condizione.

La selezione può essere :

• singola : se la condizione è vera (+) esegui un blocco di istruzioni, altrimenti (-) non fare nulla e vai avanti
• binaria : se la condizione è vera (+) esegui il blocco then, altrimenti (-) esegui il blocco else
• multipla - switch : controlla il valore di una variabile, se combacia con il caso 1 esegui il blocco 1, se combacia con il caso 2 esegui il blocco 2 e così via, se non combacia con nessun caso esegui il blocco default

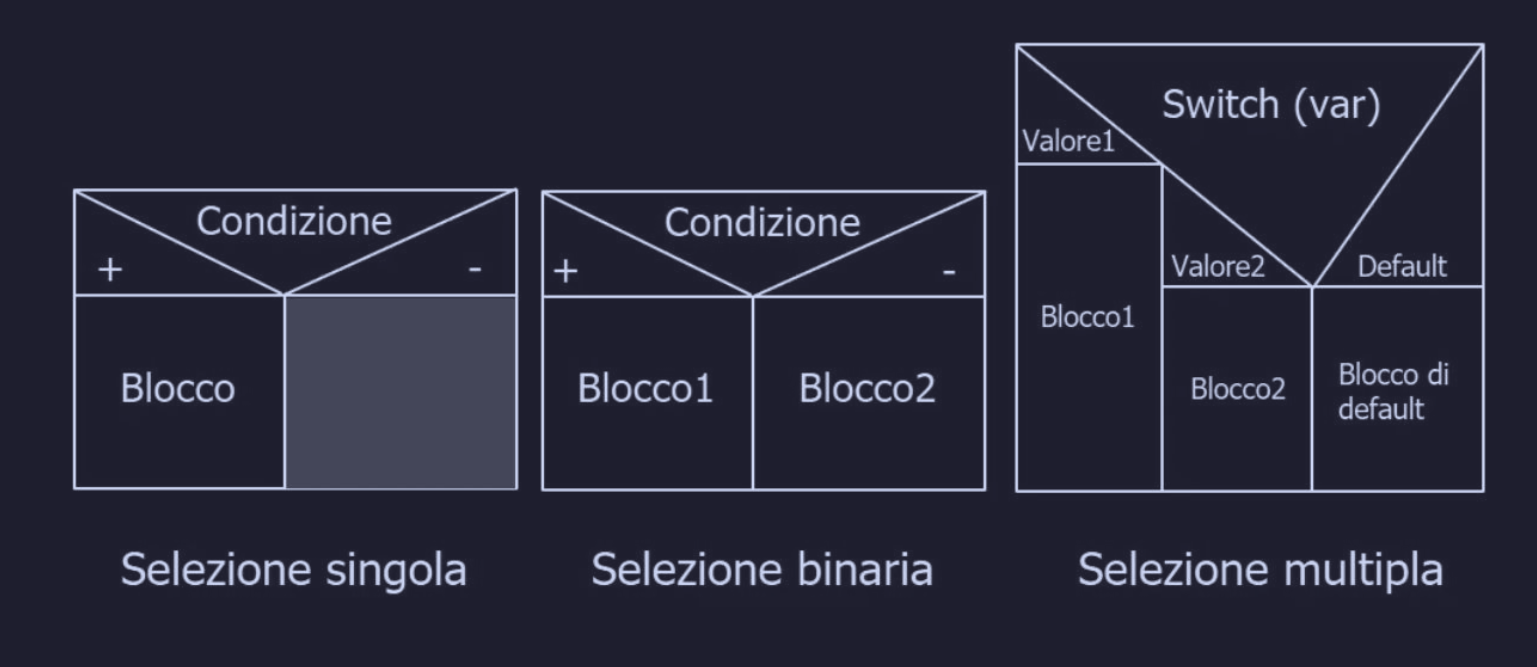
La traduzione dei blocchi di selezione in Java/C++ è la seguente :

• selezione singola :

if (<condizione>){
	// <blocco then>
}

• selezione binaria :

if (<condizione>){
	// <blocco then>
} else {
	// <blocco else>	
}

• selezione multipla :

switch (<variabile>){
	case <valore 1> :
		// <blocco 1>; 
		break;
	case <valore 2> :
		// <blocco 2>; 
		break;
	default : 
		// <blocco default> 
		break; 	
}

Iterazione

L’iterazione esprime la possibilità di ripetere l’esecuzione di un blocco interno finché è verificata una condizione. Esistono 3 tipologie di blocchi iterativi :

• for : quando è noto a priori il numero di ripetizioni da compiere
• while : quando il numero di ripetizione non è noto a priori e c’è la possibilità che il blocco interno non venga eseguito
• do-while : simile al while, ma in questo caso il blocco interno viene eseguito almeno una volta

Semplificazione dell’algoritmo merge con algebra di Boole

Consideriamo quindi l’algoritmo merge attraverso i diagrammi NS :

Ora ci domandiamo se è possibile semplificare in qualche modo, attraverso l’utilizzo di una sola selezione :

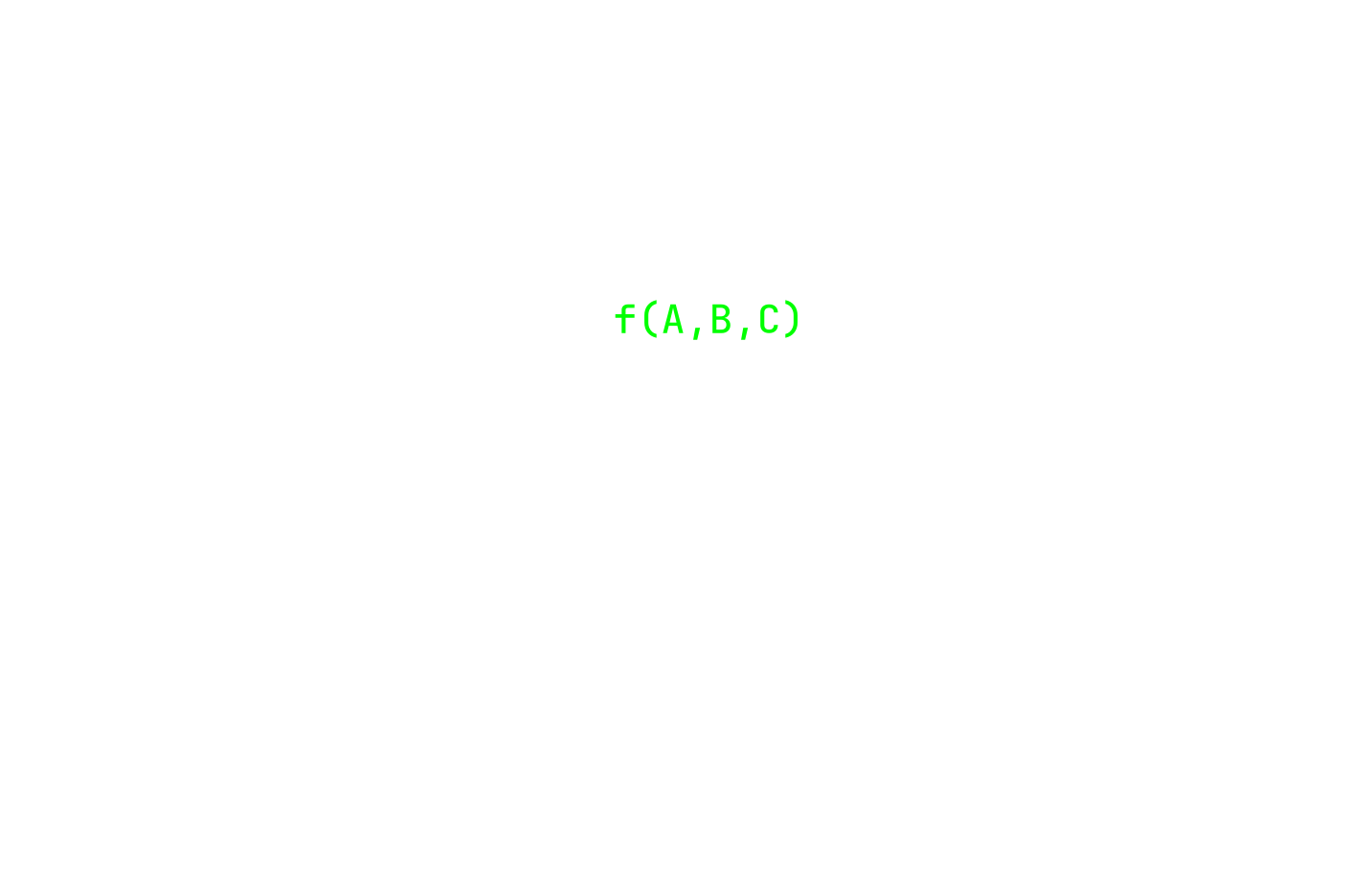
Si possono definire quindi 3 variabili logiche :

$$\{\begin{array}{l}\text{A}=\text{v[i] < w[j]}\\ \text{B}=\text{i}\le \text{n}\\ \text{C}=\text{j}\le \text{m}\end{array}$$

che saranno i parametri della funzione $f$, che determinerà in base a queste variabili se :

• copiare l’elemento corrente da v in z (output 1)
• copiare l’elemento corrente da w in z (output 0)

Quindi dobbiamo esplorare in modo esaustivo tutti i casi :

$\text{A}$	$\text{B}$	$\text{C}$	Situazione	Azione	$f$
0	0	0	v e w sono terminati	niente	X
0	0	1	v è terminato	z[k]=w[j]	0
0	1	0	w è terminato	z[k]=v[i]	1
0	1	1	v[i] >= w[j] e che i 2 array non sono terminati	z[k]=w[j]	0
1	0	0	v e w sono terminati	niente	X
1	0	1	v è terminato	z[k]=w[j]	0
1	1	0	w è terminato	z[k]=v[i]	1
1	1	1	v[i] < w[j] e che i 2 array non sono terminati	z[k]=v[i]	1
ora possiamo utilizzare le mappe di K. per ottenere una formula di $f$ semplificata ai minimi termini :

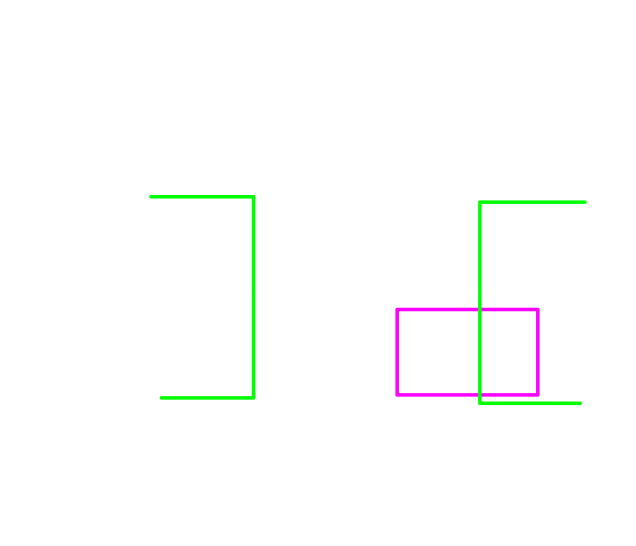quindi otteniamo la seguente formula semplificata :

$$f=\text{AB}+\overline{\text{C}}$$

quindi nel diagramma NS possiamo scrivere la condizione della selezione come :

$$f=\text{( i <= n \&\& v[i] < w[j] ) || j > m}$$

---

NS Diagrams to ARM