Fino ad ora abbiamo supposto che il segnale sia istantaneo da una porta logica ad un’altra. In realtà non è cosi , infatti la velocità massima con cui un segnale si può propagare è la velocità della luce ( circa ). Anche i processori vanno ad una velocità massima , circa . Ma cosa vuol dire che un processore va a quella velocità ? Se considero un circuito sequenziale del genere :
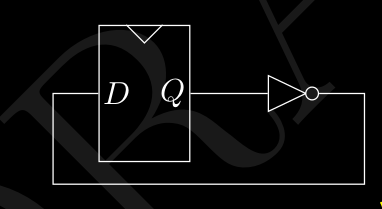
Se questo FlipFlop va a , vuol dire che il segnale del clock passa da 0 a 1 , volte al secondo. Quindi se consideriamo che il segnale da a viaggia alla velocità della luce , mi devo preoccupare che il segnale da faccia in tempo a tornare a , prima che il clock sia passato da 0 a 1 . Quindi quanto può essere lungo , al massimo, il filo che collega a ? ( un po di fisica ) :
Quindi vediamo se possiamo ottimizzare i nostri circuiti , considerando questo fatto.
Se prendiamo il circuito sommatore :
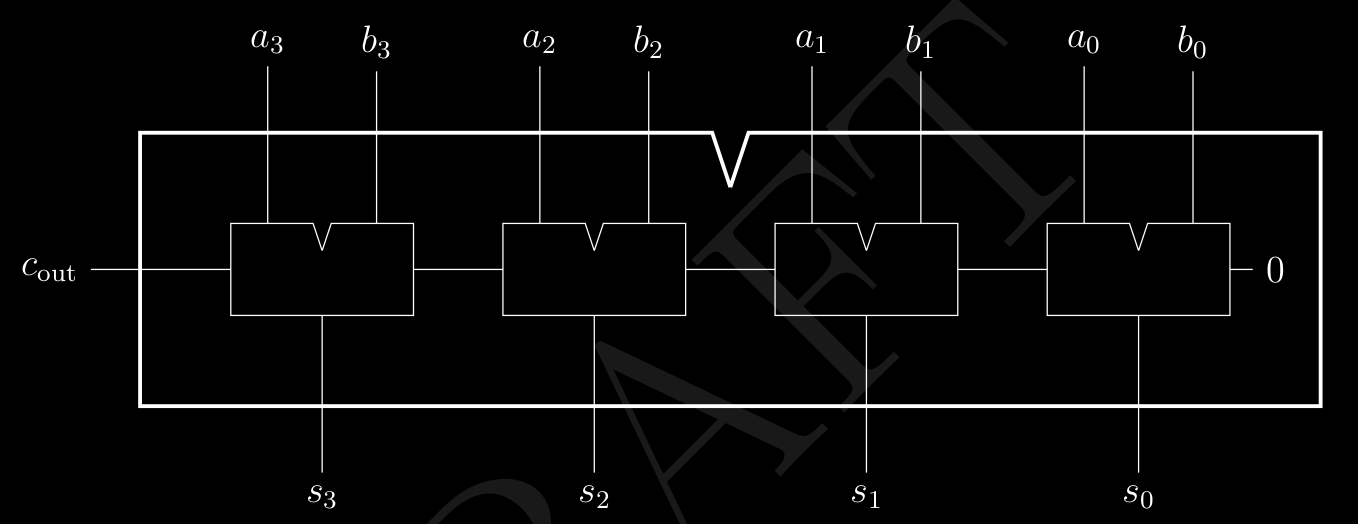
partendo dal circuito del Full-Adder :
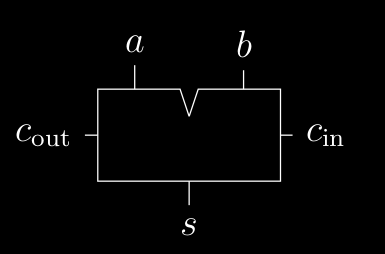
E abbiamo visto come fare il sottrattore ( differenza tra 4 bit ) :
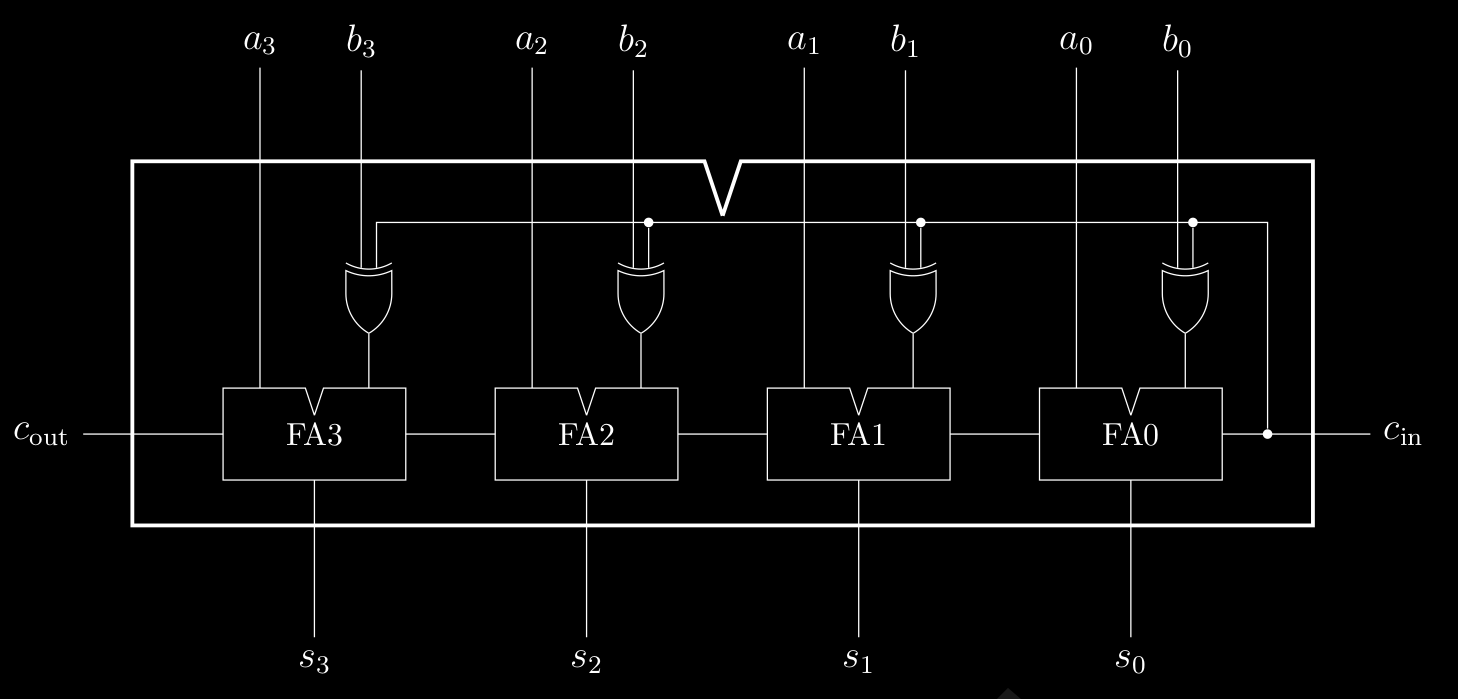
Il problema sta nel fatto che FA1 deve aspettare che FA0 , gli dia il riporto in entrata cosi che possa lavorare anche lui , stessa cosa per FA2 e cosi via . Ok per 4 bit possiamo aspettare , ma se passiamo ad un processore a 64 bit … Diventa un problema serio. Dobbiamo ottimizzare la propagazione del riporto , infatti questo di adesso viene chiamato RIPPLE-CARRY ADDER ( adder a propagazione di riporto ).
Adder ad anticipazione di riporto
Consideriamo un adder a 16 bit , e guardiamolo come 4 blocchi da 4 input :

Diamo un nome ai riporti che escono dagli Adder a 4-bit : siccome “dentro” Adder 0 è come se ci fossero quattro FA , abbiamo che esce dal primo FA , esce dal secondo FA , esce dal terzo e poi esce dal quarto e ultimo FA. Quindi all’uscita del primo adder a 4-bit avremo , e cosi via per gli altri ( come mostrato qua sopra ).
Ora siccome per terzo Adder ( vale la stessa cosa per il secondo e in su ) , per poter iniziare a lavorare , deve aspettare che il secondo Adder ( quello prima di lui ) gli dia , però il tempo che gli arriva questo è diciamo lungo, siccome deve passare a sua volta dentro altri 4 FA ( interni del secondo Adder ) .
Allora l’obiettivo è “darglielo in qualche modo prima” invece di farlo passare per tutti i 4 FA interni , ovvero che quando al secondo Adder quando gli arriva il suo , possiamo determinare “direttamente” chi è , facendolo con il minor numero possibile di porte logiche.
Per capire come poter implementare questa ottimizzazione , osserviamo cosa fa un FA da solo , e domandiamoci quando genera un riporto ? :
- sicuramente quando gli input e sono ⇒ FA genera il riporto
- quando uno solo dei due ( o ) è ( quindi ) ⇒ FA propaga il riporto
quindi possiamo scrivere che il mio riporto ( successivo ) sarà generato da FA o propagato da FA : dove nell’ultimo ci siamo fregati dello siccome lo xor dice che devono essere diversi e fa , ma se sono diversi , pero con or faranno , stessa cosa per il contrario , se è falso xor ( se sono tutti e due ) allora sarà vero l’and e quindi sarà .
Per comodità scriviamo ( generazione del riporto ) e ( propagazione del riporto ) , quindi la nostra relazione di ricorrenza sarà :
Quindi adesso per sapere come posso determinare “direttamente” , devo metterlo in funzione di :
a sua volta però , insomma abbiamo capito e dobbiamo arrivare a :
notiamo infatti che se e dipendono solo da e , il nostro Adder con e può “subito” fare parte del lavoro , poi appena gli arriva può determinare “immediatamente” facendo l’and , infatti possiamo scrivere che :
quindi per determinare , passa solo per due porte AND , infatti il circuito diventa :
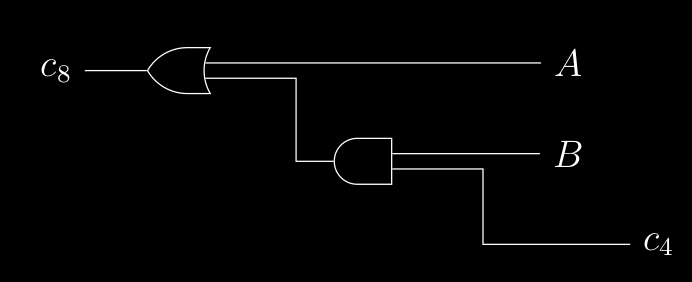
Qui abbiamo ottimizzato dividendo a blocchi da 4 un sommatore a 16 bit , ma questo lo possiamo fare ricorsivamente , infatti quello da 64 bit è fatto da 4 pezzi da 16.
