Macchine a stati finiti

Nella logica sequenziale abbiamo detto che l’uscita dipende sia dai valori correnti che dai valori precedenti , ma la differenza principale sta tra sincrone e asincrone.

• Sincrone : tutti gli aggiornamenti sono sincronizzati da un clock ( consideriamo solo questo ora )
• Asincrone : gli stati cambiano non appena gli ingressi cambiano ( come il latch-D )

Quelle sincrone possono essere rappresentate in questo modo :

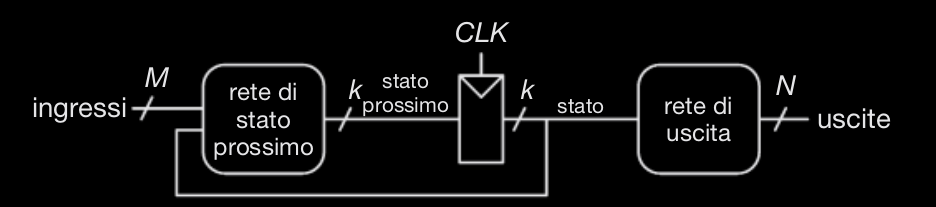
queste forme si chiamano macchine a stati finiti o FSM. Si chiamano cosi’ perché effettivamente una macchina con $k$ registri può trovarsi in $2^k$ di stati diversi. Inoltre una FSM ha $M$ input , $N$ output e $k$ bit di stato. Inoltre riceve un segnale di clock e a volte anche un segnale di reset. Una FSM è composta da un blocco di logica dello stato prossimo , uno per la logica di uscita e da un registro che “memorizza” lo stato. Ad ogni fronte di salita di clock la FSM avanza allo stato prossimo definito in base agli input e allo stato corrente.

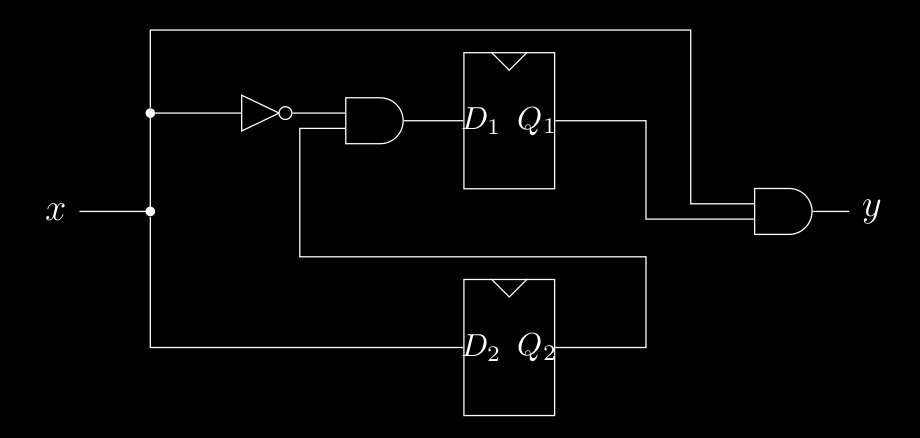
Supponiamo per esempio di avere questo circuito :

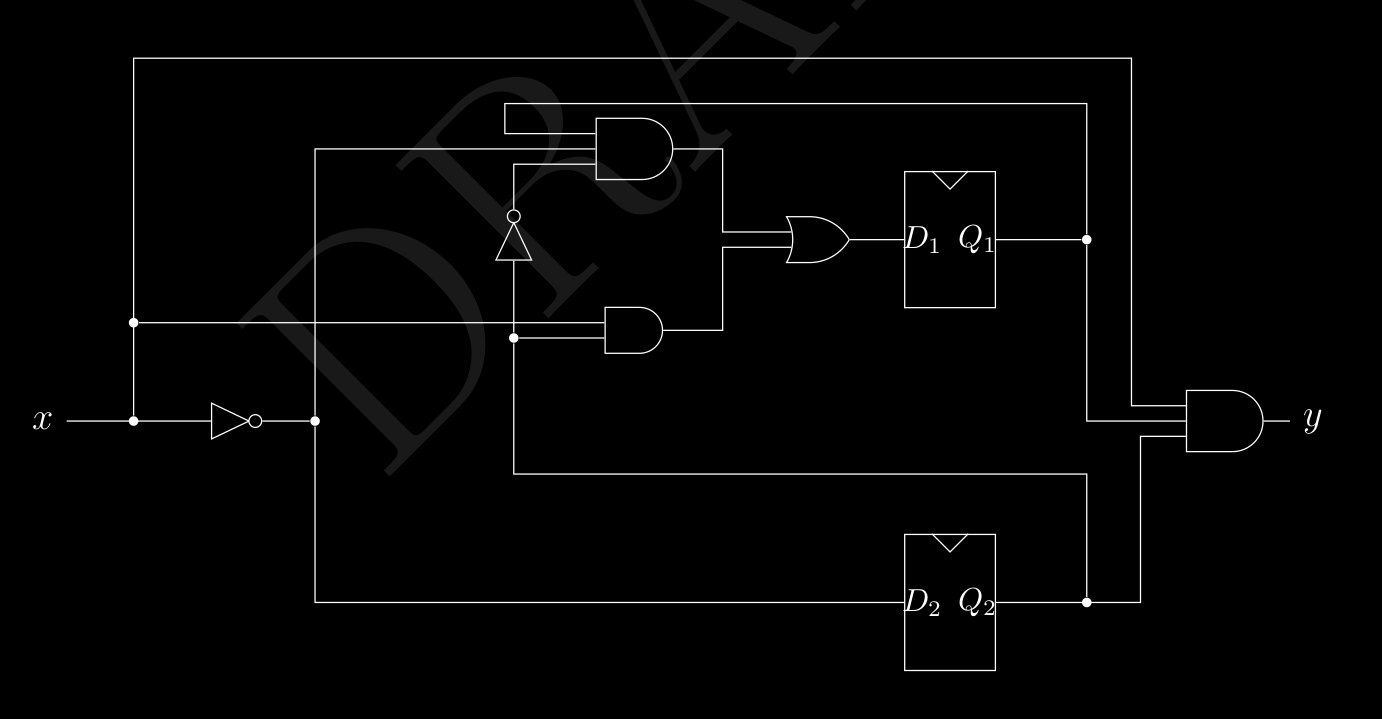
che contiene la seguente roba :

• un registro formato da 2 FlipFlop che hanno degli stati futuri ( $D_1,D_2$ ) e gli stati attuali ( $Q_1,Q_2$ )
• porte logiche elementari
• input $x$
• output $y$

Ora , siccome sappiamo che $Q_1,Q_2$ sono lo stato attuale del circuito , quindi appena passiamo $x$ in questo attuale stato , sappiamo per certo gli stati futuri $D_1,D_2$ (siccome a loro due entrano una parte di $x$ ) , che l’output $y$ . Quindi siccome $x,Q_1,Q_2$ sono le variabili indipendenti e $y,D_1,D_2$ sono le variabili dipendenti , possiamo rappresentare il circuito attraverso un’equazione di stato :

$$\{\begin{array}{l}{D}_1=Q_{2}x+Q_1\overline{Q_2}\overline{x}\\ D_2=\overline{x}\\ y=Q_2{Q}_{1}x\end{array}$$

a sua volta ( siccome sta roba nell’equazione di stato sono formule della logica proposizionale ) possiamo ottenere la tabella di stato :

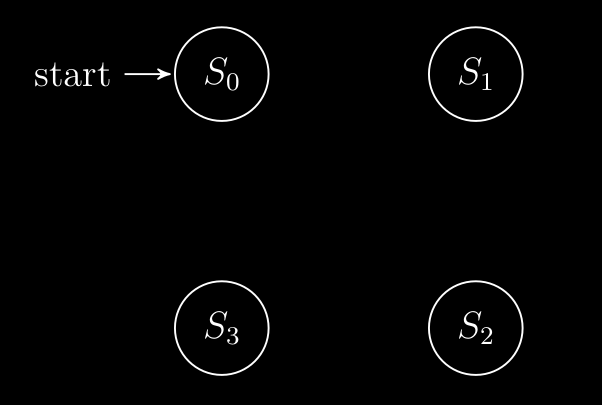
Possiamo ancora rappresentare il circuito , attraverso il diagramma di stato , ovvero un grafo diretto dove :

• nodi : rappresentano i vari stati del circuito ( indicati con $S_i$ con $i=0,1,\dots ,2^k-1$ , ovvero tutti i possibili stati che può assumere il circuito )
• archi : transizioni da uno stato all’altro
• etichette degli archi : input che determinano le transazioni e output attuali del circuito ( formato : $x/y$ )

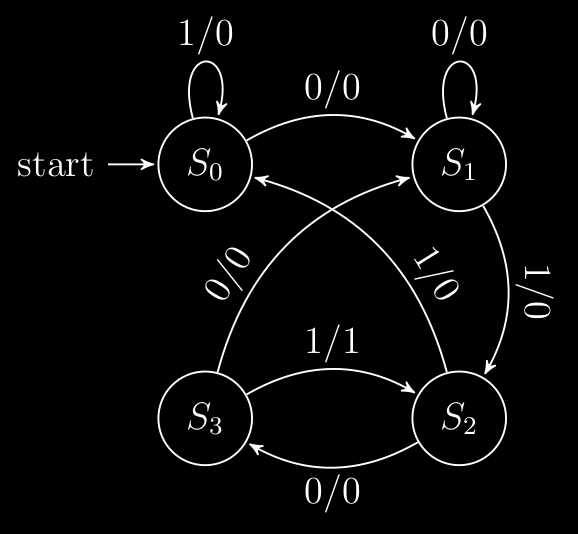
Quindi nel nostro circuito il diagramma di stato ha come stati :

$$S_0=(0,0),S_1=(0,1),S_2=(1,0),S_3=(1,1)$$

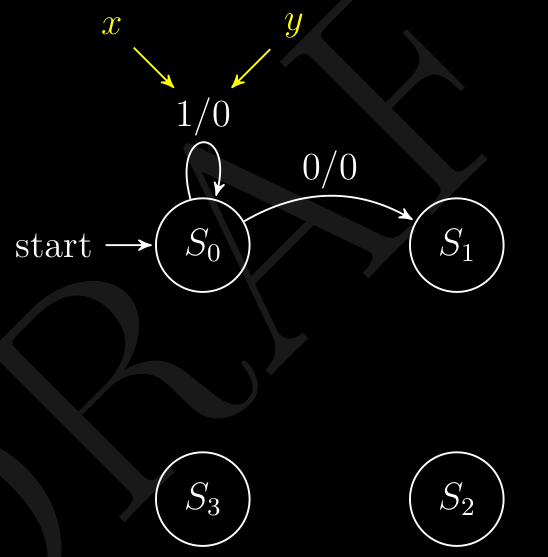
e quindi possiamo iniziare a disegnare il diagramma di stato secondo la tabella di stato , infatti all’inizio ( start ) il circuito partirà da $S_0=(Q_1,Q_2)=(0,0)$ e quindi avremo due “casi di input” :

• se $x=0$ ⇒ il circuito passerà ad uno stato $(0,1)$ ovvero $S_1$ e da in output $y=0$
• se $x=1$ ⇒ il circuito passerà ad uno stato $(0,0)$ ovvero $S_0$ ( se stesso ) e da in output $y=0$ e quindi otteniamo :

Andando avanti così fino a $S_3$ otteniamo :

Ma a cosa serve tutto questo? Beh serve quando vogliamo costruire un circuito che faccia della roba , e quindi possiamo partire dal diagramma di stato e andando a ritroso di come abbiamo fatto adesso , otteniamo si un circuito diverso da un’altro che fa la stessa cosa , ma farà la stessa cosa anche lui.

Supponiamo per esempio di voler progettare un circuito che ad ogni ciclo di clock , gli venga passato un input $x$ e restituisca $1$ se e solo se gli ultimi 3 bit letti formano la sequenza $101$ .

Per esempio supponiamo che per i primi $t=1,2,3,\dots ,10$ cicli di clock , venga passata questa sequenza in input $x$ e con il rispettivo output $y$ :

$$\begin{array}{cccccccccccc}t& 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \cdots \\ x& 1& 1& 0& 1& 0& 1& 1& 0& 0& 1& \cdots \\ y& 0& 0& 0& 1& 0& 1& 0& 0& 0& 0& \dots \end{array}$$

Beh costruire questo circuito direttamente con porte logiche elementare , FlipFlop etc.. sarebbe un’impresa , però possiamo fare cosi : diagramma di stato → tabella di stato → equazioni di stato → circuito.

Vediamo allora come fare il diagramma di stato. Sicuramente il nostro circuito partirà da uno stato $S_0$ :

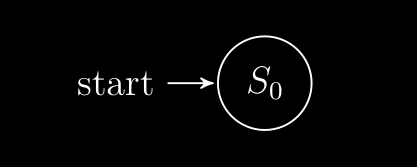
Poi dallo stato $S_0$ l’input $x$ può essere $0$ o $1$ :

• se $x=0$ ⇒ beh questo è il primo bit che leggiamo quindi la nostra sequenza ( che chiamerò $d$ ) sarà $d=0$ , quindi è come se stiamo ancora “fermi” e non cambiamo stato , quindi lo stato non cambia e torna su se stesso e come output ritorniamo $0$ .
• $x=1$ ⇒ beh ora cambia la situazione , infatti se $d=1$ vuol dire che abbiamo iniziato a leggere ( “costruire” ) la nostra sequenza voluta , quindi cambiamo stato in $S_1$ e come output ritorniamo $0$ .

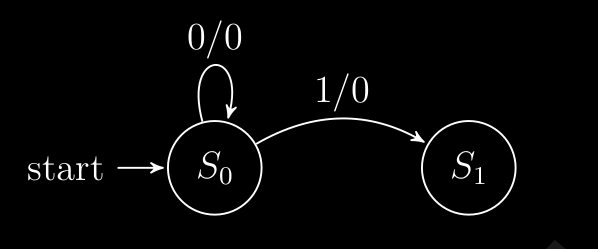
Ora stiamo in $S_1$ e quindi vuol dire che la nostra $d=1$ , e abbiamo sempre due casi di $x$ :

• se $x=0$ ⇒ ottimo la nostra $d$ diventa $d=10$ e quindi dobbiamo cambiare stato , siccome stiamo costruendo la nostra sequenza voluta.
• se $x=1$ ⇒ non va bene perché la nostra $d$ diventa $d=11$ , quindi in che stato andiamo? beh se ci ragioniamo $1$ potrebbe essere un candidato di una nuova costruzione che porterebbe alla nostra sequenza voluta , quindi rimaniamo in questo stato $S_1$ e la nostra $d$ rimane quindi $d=1$ . ( in tutti e due i casi $y=0$ siccome ancora non abbiamo ottenuto la nostra sequenza voluta )

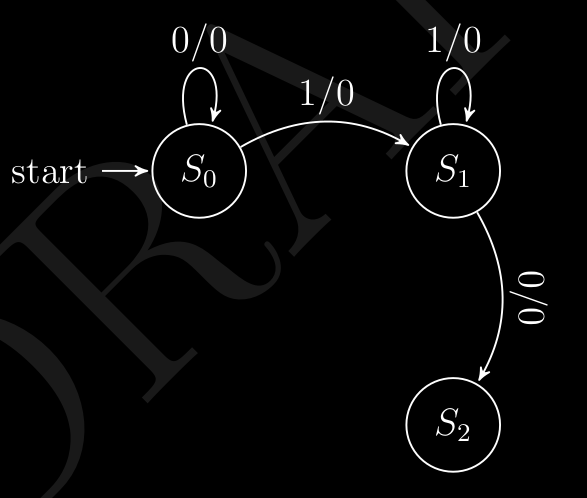
Ora stiamo in $S_2$ e quindi la nostra $d=10$ , anche qui i due casi :

• se $x=0$ ⇒ non va bene , la nostra $d$ diventa $d=100$ e quindi dobbiamo necessariamente tornare al punto di partenza $S_0$ perché abbiamo distrutto la nostra sequenza voluta e torniamo output $0$ .
• se $x=1$ ⇒ ottimo , otteniamo la nostra sequenza voluta ( $d=101$ ) e quindi dobbiamo restituire in output $1$ e torniamo nello stato $S_1$ , siccome questo nuovo $1$ potrebbe aiutarci ancora .

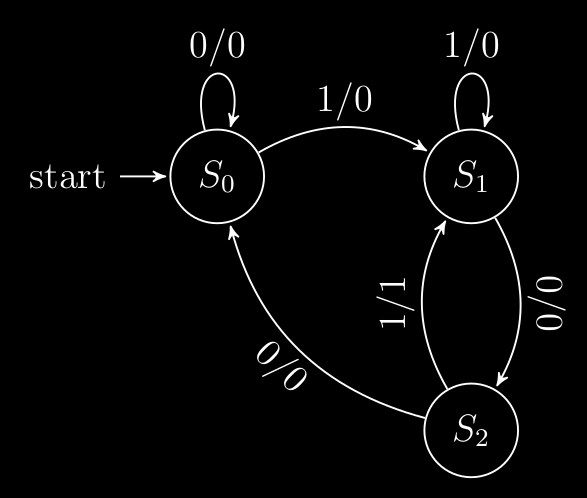
Ora abbiamo finito , e iniziamo a fare la tabella di stato. Siccome abbiamo 3 stati $S_0,S_1,S_2$ , avremo necessariamente bisogno di un registro a 2 bit siccome sappiamo che a 2 bit potrà avere $2^2=4$ stati , questo implica che dovremmo usare 2 FlipFlop . Ora se codifichiamo ( scelta arbitraria , come vedremo dopo ) i nostri stati in questo modo :

$$\{\begin{array}{l}{S}_0=(0,0)\\ S_1=(0,1)\\ S_2=(1,0)\end{array}$$

e indichiamo gli stati attuali con $Q_1,Q_2$ e futuri con $D_1,D_2$ dei due FlipFlop , otteniamo la seguente tabella# di stato :

$$\begin{array}{ccccccc}{Q}_1& Q_2& x& & D_1& D_2& y\\ 0& 0& 0& & 0& 0& 0\\ 0& 0& 1& & 0& 1& 0\\ 0& 1& 0& & 1& 0& 0\\ 0& 1& 1& & 0& 1& 0\\ 1& 0& 0& & 0& 0& 0\\ 1& 0& 1& & 0& 1& 1\\ 1& 1& 0& & X& X& X\\ 1& 1& 1& & X& X& X\end{array}$$

Siccome la nostra FSM non andrà mai nello stato $S_4=(1,1)$ ( che neanche esiste infatti ) , non è rilevante cosa assegniamo a $D_1,D_2$ e $y$ in corrispondenza di quelle righe ( infatti ho messo una $X$ ).

Ora è tutto in discesa , perché sappiamo ricavare da una tabella di verità una formula grazie alle mappe di Karnaugh :

• per $D_1$ : $$\begin{array}{ccccc}x/Q_1{Q}_2& 00& 01& 11& 10\\ 0& 0& 1& X& 0\\ 1& 0& 0& X& 0\end{array}$$ quindi da $1,X$ ( siccome $X$ possiamo manipolarla come ci pare ) ( non ha senso prendere anche $X,X$ siccome dobbiamo raggruppare con degli $1$ già presenti ) , quindi otteniamo che : $$D_1=\overline{x}{Q}_2$$
• per $D_2$ si nota già dalla tabella di stato che sarebbe : $$D_2=\overline{x}$$
• per $y$ : $$\begin{array}{ccccc}x/Q_1{Q}_2& 00& 01& 11& 10\\ 0& 0& 0& X& 0\\ 1& 0& 0& X& 1\end{array}$$ e quindi otteniamo con $X,1$ : $$y=Q_{1}x$$ Ora non ci resta che fare il circuito che sarebbe , secondo le equazioni di stato :

Circuiti alla Moore e alla Mealy

Le macchine a stati finiti si distinguono i due diverse tipologie :

• macchine alla Moore : dove gli output dipendono solo dallo stato presente del circuito
• macchine alla Mealy : dove gli output dipendono dallo stato presente del circuito e anche dagli input attuali ( nei casi di prima la variabile $x$ ).

le macchine a stati finiti infatti possiamo rappresentarle in questo modo :

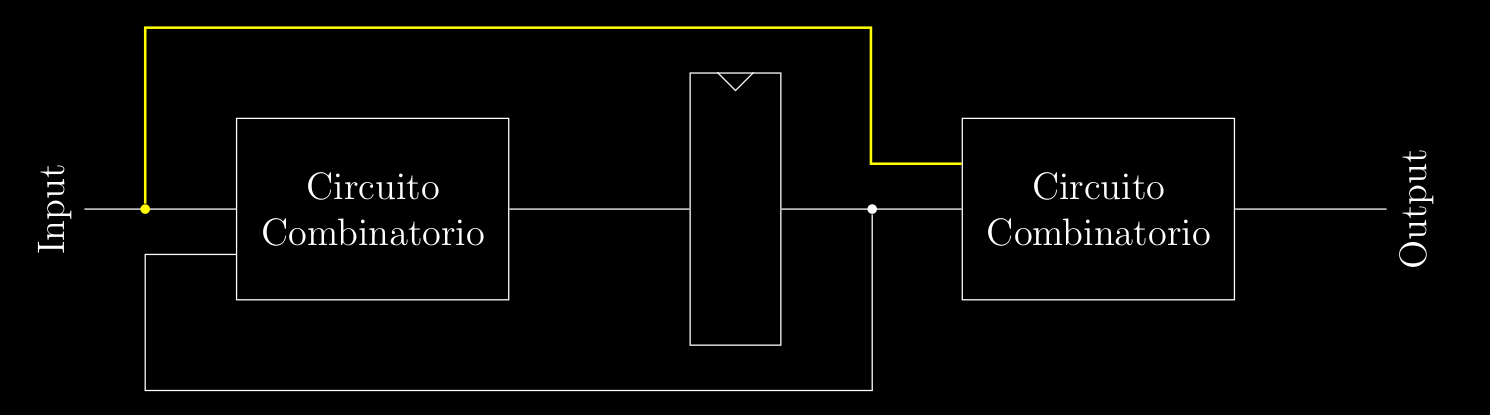
dove la linea gialla indica che si sta parlando di una macchina alla Mealy e senza sarebbe alla Moore ( dove infatti l’output dipende solo dallo stato dei registri ) , infatti fino ad ora abbiamo visto macchine alla Mealy . La differenza quindi sostanziale che c’è tra i due è che nella macchine alla Moore , i singoli stati il loro output dipende solo dallo stato attuale e non dall’input , quindi l’output nel cerchietto è già determinato dallo stato. Notiamo quindi che si abbiamo due casi nei singoli stati , ma nei singoli stati l’output è già deciso dallo stato attuale , quindi ci serviranno più stati.

Per esempio supponiamo di voler progettare la macchina a stati finita che legge una sequenza infinita di bit in input e ritorna $1$ se e solo se gli ultimi 3 bit formano la sequenza $101$ , però sta volta facciamola alla Moore. Partiamo quindi dal diagramma di stato :

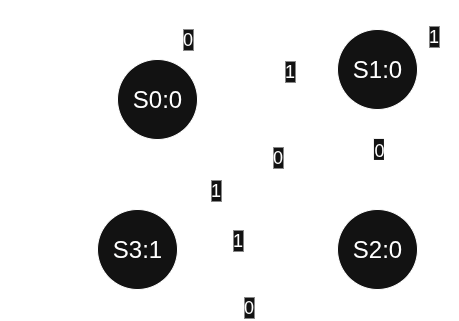
notiamo infatti che abbiamo utilizzato uno stato in più della macchina alla Mealy , gli stati si trovano nel formato $(S_i:y)$ dove $y$ è proprio l’output già determinato dallo stato attuale. Ora facciamo la tabella di stato , siccome $y$ è determinato solo dagli stati attuali $Q_1,Q_2$ , ci servono solo loro per avere $y$ :

$$\begin{array}{cccc}{Q}_1& Q_2& & y\\ 0& 0& & 0\\ 0& 1& & 0\\ 1& 0& & 0\\ 1& 1& & 1\end{array}$$

quindi notiamo subito che l’equazione di stato di $y$ è $y=Q_1{Q}_2$ . Ora ci serve la tabella di stato di $D_1,D_2$ per ottenere questi ci servono $Q_1,Q_2,x$ :

$$\begin{array}{cccccc}{Q}_1& Q_2& x& & D_1& D_2\\ 0& 0& 0& & 0& 0\\ 0& 0& 1& & 0& 1\\ 0& 1& 0& & 1& 0\\ 0& 1& 1& & 0& 1\\ 1& 0& 0& & 0& 0\\ 1& 0& 1& & 1& 1\\ 1& 1& 0& & 1& 0\\ 1& 1& 1& & 0& 1\end{array}$$

quindi per $D_2$ si nota subito che la sua equazione sarebbe $D_2=x$ , mentre per $D_1$ bisogna fare la mappa di Karnaugh , da cui otteniamo che $D_2=Q_2\overline{x}+Q_0\overline{Q_1}x$ . Quindi ora risulta facile costruire il circuito secondo le equazioni di stato appena ottenute.